2 R Basics II: Datenstrukturen

Bisher haben wir Variablen als Platzhalter für Werte vom Typ character, integer, numeric oder logical genutzt. Variablen können aber auch Platzhalter für strukturierte Sammlungen von Werten sein. Datenstrukturen können anstelle von einfachen Werten auch selbst wieder Datenstrukturen enthalten. Die verschiedenen Weisen, wie Daten in R organisiert und im Speicher repräsentiert werden können, werden Datenstrukturen genannt. Solche Datenstrukturen können entweder nur Elemente vom selben Typ aufnehmen (wie z.B. Vektoren und Matrizen), oder Elemente unterschiedlichen Typs (wie z.B. Listen und Dataframes). Wir werden in diesem Kapitel alle wichtigsten Datenstrukturen besprechen. In der Praxis werden wir aber vor allem mit Vektoren und Dataframes arbeiten.

2.1 Grundlegende Begriffe

Begriff	Englische Entsprechung	Definition (im R-Kontext)
Element	Element	Wert oder anderes Objekt innnerhalb einer Datenstruktur. Datenstrukturen können selbst Elemente einer anderen Datenstruktur sein. Elemente haben einen Index und manchmal zusätzlich einen Namen (oder ‘Schlüssel’), über den auf das Element zugegriffen werden kann.
Index	Index	Position eines Elements innerhalb einer Datenstruktur. Ein Index ist in R immer eine Zahl >= 1.
Indexierung	Indexing	Überbegriff für verschiedene Operationen, mit denen auf Elemente in einer Datenstruktur zugegriffen werden kann.
Zugreifen	Access	Operation, bei der durch den Einsatz spezifischer Operatoren Elemente einer Datenstruktur ausgewählt, diese extrahiert oder modifiziert werden können.
Vektorisierung	Vectorization	Mechanismus, bei dem Funktionen oder Operationen automatisch auf alle Elemente eines Vektors angewandt werden, statt auf einzelne Elemente.
Dimension	Dimension	In Bezug auf Matrizen die Anzahl von Zeilen und Spalten (angegeben als Zeilen x Spalten). In Bezug auf Arrays allgemein die Anzahl der verschiedenen ‘Richtungen’, in denen Daten organisiert sind. Bei einem Array können das nicht nur Zeilen und Spalten sein, sondern auch ‘Schichten’ von Matrizen und andere Organisationsweisen.

2.2 Vektoren

Eigentlich haben wir in der letzten Stunde schon Vektoren kennengelernt. Denn in R ist jeder einzelne Wert zugleich ein Vektor der Länge 1. Vektoren sind nämlich im Grunde Sequenzen verschiedener Werte desselben Datentyps. Die Werte innerhalb eines Vektors werden Elemente genannt. Die Elemente in einem Vektor haben eine festgelegte Reihenfolge. Jedes Element in einem Vektor hat deswegen eine Position (auch “Index” genannt) zwischen 1 und n, wobei n eine beliebige ganze Zahl > 1 ist. Über den Index kann auf jedes Element einzeln zugegriffen werden oder es können mehrere Elemente gleichzeitig ausgewählt werden. Der Zugriff auf Elemente des Vektors erfolgt mithilfe von eckigen Klammern und wird im Abschnitt 2.2.4 erläutert.

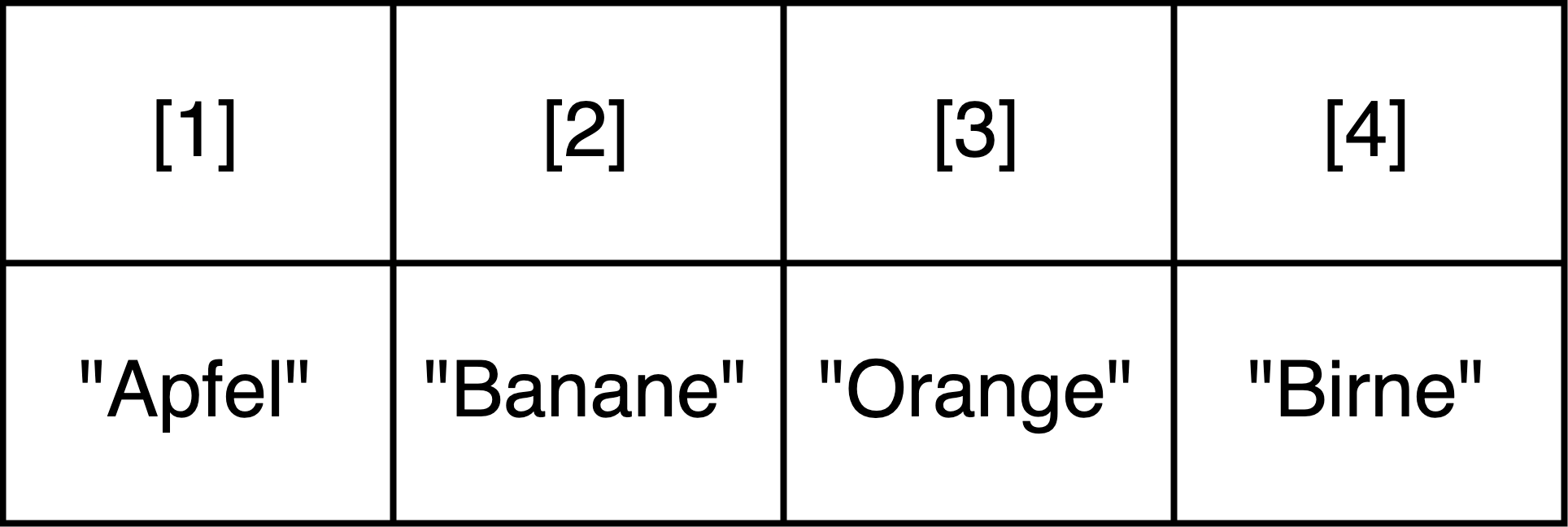
2.2.1 Vektoren erstellen

Vektoren können mithilfe von bestimmten Funktionen (lernen wir noch) erstellt werden. Wenn bei der Erstellung bekannt ist, welchen Datentyp die Elemente haben sollen, können die Funktionen character() oder numeric() zur Erstellung verwendet werden. Im Regelfall ist aber die Anzahl der Elemente und/oder deren Datentyp bei der Erstellung noch nicht bekannt. In diesem Fall wird zur Erstellung eines leeren Vektors die Funktion c() verwendet:

# leeren Vektor erstellen, ohne einen bestimmten Datentyp festzulegen
c()

#> NULL

Wenn ein leerer Vektor erstellt wird, wird dieser mithilfe des Werts NULL repräsentiert. Darauf kommen wir am Ende der Sitzung noch einmal zurück.

Mithilfe der Funktion c() können auch Vektoren aus bereits bekannten Elementen erstellt werden:

# Vektor aus einer Zahlsequenz erstellen
zahlen <- 1:3
print(zahlen)

#> [1] 1 2 3

# Vektoren mit selbst gewählten Elementen erstellen 
leckere_fruechte <- c("Apfel", "Banane", "Erdbeere")
coole_zahlen <- c(45, 7, 420)

Vektoren können auch durch Zusammenfügen zweier bestehender Vektoren erstellt werden. Wenn die Funktion c() auf zwei Vektoren oder einen Vektor und ein Element angewandt wird, dann werden die beiden Vektoren in der angegebenen Reihenfolge in einen neuen Vektor kombiniert:

# Vektoren kombinieren mithilfe der Funktion c()
fruechte_und_zahlen <- c(leckere_fruechte, coole_zahlen) 
# Vektor auf dem Bildschirm ausgeben
print(fruechte_und_zahlen)

#> [1] "Apfel"    "Banane"   "Erdbeere" "45"       "7"        "420"

Achtung: Bei der Erstellung von Vektoren muss beachtet werden, dass der Typ der Elemente automatisch vereinhetilicht wird, wenn Elemente mit unterschiedlichen Datentypen in einen Vektor kombiniert werden:

vec <- c("hallo", "1")
vec <- c(vec, 3)
# double wird zu character
typeof(vec)

#> [1] "character"

# bool wird zu double
vec <- c(3, TRUE)
typeof(vec)

#> [1] "double"

Nur, wenn ein Element des Vektors eine Liste ist, gilt dieses Prinzip nicht. Darauf kommen wir im Abschnitt “Listen” noch einmal zurück.

Während es jeden Index nur einmal gibt, können sich die Werte in einem Vektor wiederholen:

fruechte <- c("Apfel", "Apfel", "Orange")

In diesem Vektor gibt es den Wert “Apfel” zwar zweimal, aber die Werte haben verschiedene Indexpositionen (1 bzw. 2).

2.2.2 Sets (Mengen)

In anderen Programmiersprachen (bspw. Python) gibt es eine Datenstruktur, die oft Set (Menge) genannt wird. Sets (Mengen) sind dadurch ausgezeichnet, dass alle Werte einzigartig sind. In R gibt es keine eigenständige Datenstruktur für Mengen. Dennoch ist es möglich und oft nützlich, in R mit Sammlungen von einzigartigen Werten zu arbeiten und Mengenoperationen durchzuführen. In R können Mengen aus Vektoren erstellt werden, indem die einzigartigen Werte eines Vektors oder mehrerer Vektoren extrahiert werden:

# Einzigartige Werte eines Vektors ausgeben lassen
unique(c("Apfel", "Banane", "Erdbeere", "Apfel"))

#> [1] "Apfel"    "Banane"   "Erdbeere"

# Vereinigung von zwei Vektoren: 
union(c("Apfel", "Banane", "Erdbeere", "Apfel"), c("Kiwi", "Grapefruit"))

#> [1] "Apfel"      "Banane"     "Erdbeere"   "Kiwi"       "Grapefruit"

# Schnittmenge von zwei Vektoren: 
intersect(c("Apfel", "Banane"), c("Erdbeere", "Apfel"))

#> [1] "Apfel"

# Differenz zwischen zwei Vektoren: Elemente erhalten, die im ersten Vektor, aber nicht im zweiten Vektor vorkommen. 
setdiff(c("Apfel", "Banane"), c("Erdbeere", "Apfel"))

#> [1] "Banane"

2.2.3 Named Vectors

Neben den “einfachen” Vektoren gibt es noch sogenannte benannte Vektoren oder named vectors. Das sind Vektoren, bei dem jedem Element nicht nur eine Indexposition, sondern auch ein Name zugeordnet ist.

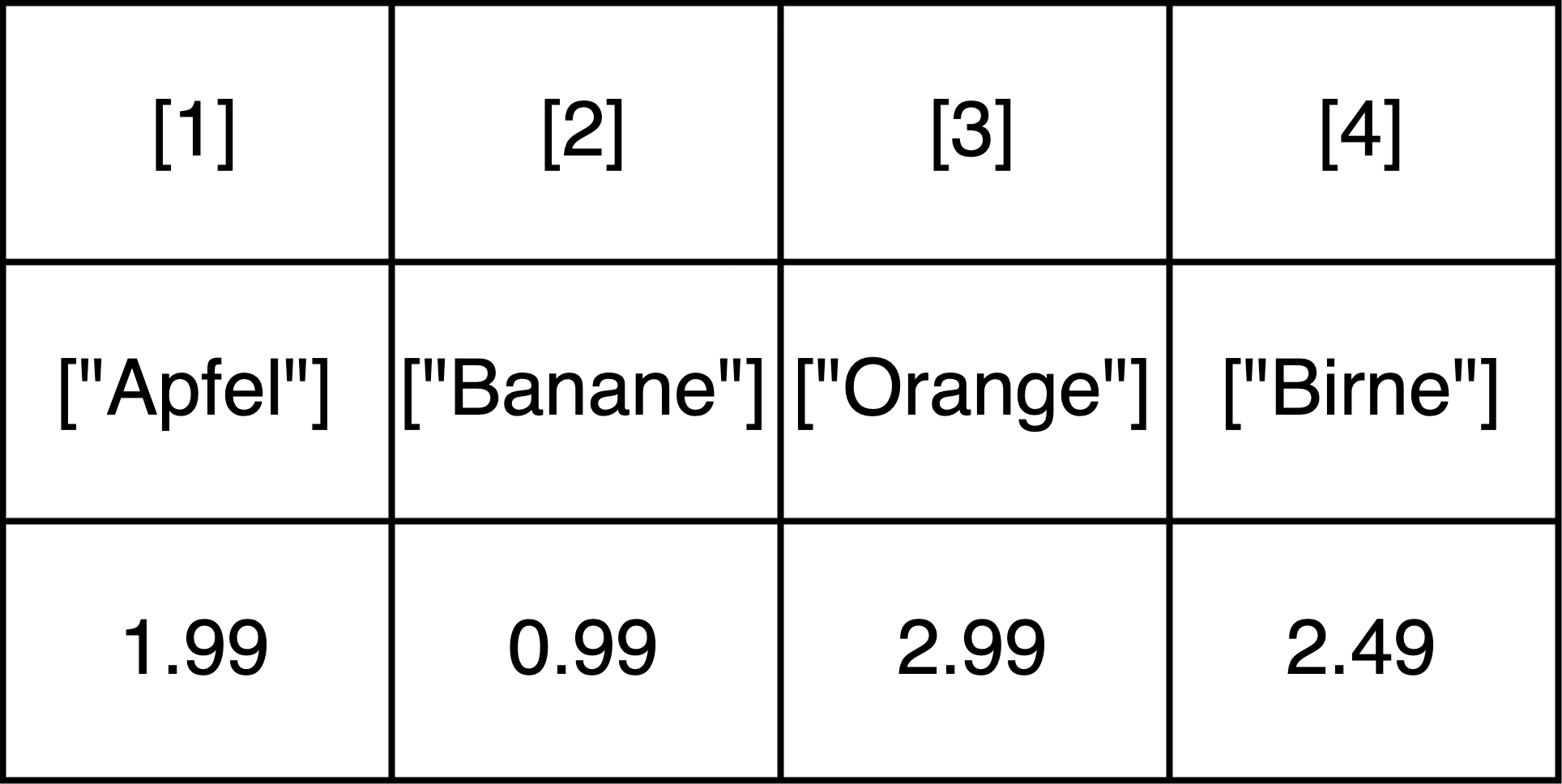
Um einen named vector zu erstellen, wird ebenfalls die Funktion c() verwendet. Den Elementen wird bei der Erstellung des Vektors aber ein Name (oder “Schlüssel”) zugeordnet. Dieser muss ein character sein. Beachtet, dass bei der Zuweisung von Namen innerhalb von Funktionen anstelle des Zuweisungsoperators <- der Operator = verwendet wird:

# Erstellung eines named vectors: Schlüssel sind immer Zeichenketten 
einkauf <- c("Apfel"=4, "Banane"=3, "Erdbeere"=20)
# ...selbst dann, wenn ihr Wörter ohne Anführungszeichen eingebt, weiß R, dass eine Zeichenkette gemeint ist: 
einkauf <- c(Apfel=4, Banane=3, Erdbeere=20)
# Das geht allerdings nicht, wenn ihr Zahlen als Schlüssel eingebt! 
# einkauf <- c(1=4, 2=3, 3=20)

2.2.4 Faktoren

Da R ursprünglich für die Statistik entwickelt wurde, haben sich die Entwickler:innen der Programmiersprache überlegt, dass es praktisch wäre, wenn es eine Datenstruktur speziell für kategorische (auch “kategoriale”) Daten gäbe. Kategorische Daten sind Daten, die in bestimmte Kategorien oder Gruppen fallen, also beispielsweise Farben, Regionen, Beschäftigungsstatus. Speziell zur Organisation solcher Daten gibt es in R Faktoren. Ein Faktor ist eine spezielle Art von Vektor, der kategorische Daten repräsentiert. Es handelt sich dabei eigentlich um einen “einfachen” Vektor, dem eine zusätzliche Metainformation hinzugefügt wurde: die Information, welche verschiedenen Arten oder Kategorien von Werten der Vektor enthält (=“Levels”).

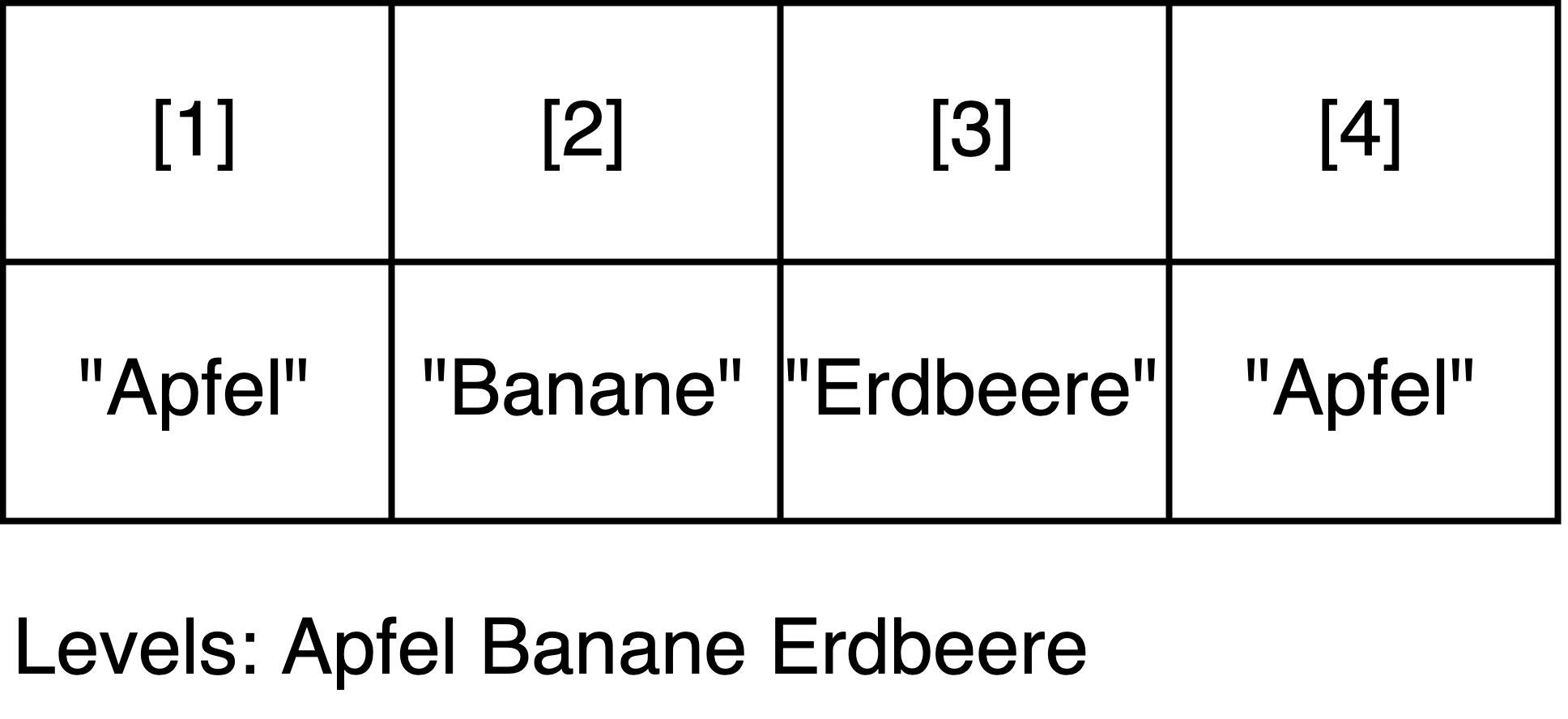
Im Beispiel oben hat der Vektor vier Elemente, aber nur drei verschiedene Elemente, nämlich “Apfel”, “Banane” und “Erdbeere”. Die Levels entsprechen also im Grunde genau den einzigartigen Werten eines Vektors, die wir im Abschnitt zu Sets (Mengen) mithilfe der Funktion unique(c("Apfel", "Banane", "Erdbeere", "Apfel")) erhalten haben. Faktoren erlauben also, sowohl die ursprünglichen, möglicherweise wiederholt vorkommenden Werte als auch die einzigartigen Werte in einem Vektor zu repräsentieren.

Faktoren werden mithilfe der Funktion factor() erstellt. Faktoren werden stets aus bereits existierenden Vektoren erstellt, beispielsweise aus dem Vektor fruechte, den wir hier noch einmal neu erstellen:

fruechte <- c("Apfel", "Banane", "Erdbeere", "Apfel")

factor(fruechte)

#> [1] Apfel    Banane   Erdbeere Apfel   
#> Levels: Apfel Banane Erdbeere

In der Praxis werden wir nicht häufig Faktoren selbst erstellen. Trotzdem solltet ihr zumindest von Faktoren gehört haben. Denn Faktoren werden in R häufig automatisch “unter der Motorhaube” beim Anwenden vieler Funktionen erstellt. Ein Beispiel dafür besprechen wir im nächsten Abschnitt. Faktoren vereinfachen viele Operationen und Berechnungen und sind einer der Gründe dafür, warum sich R von anderen Programmiersprachen unterscheidet. Deswegen sind Faktoren zum Verständnis von R und von manchen Funktionen wichtig, auch, wenn wir selbst damit nicht häufig arbeiten.

2.2.5 Operationen auf Vektoren

Wir haben gesehen, dass alle Vektoren, egal ob einfache Vektoren, benannte Vektoren oder Faktoren, Elemente in einer festgelegten Reihenfolge enthalten, Wir haben auch gesehen, dass jedes Element einen Index hat, also eine Zahl, welche die Position des Elements in dem Vektor beschreibt. Um auf ein oder mehrere Elemente in einem Vektor zuzugreifen, wird der Zugriffsoperator [] verwendet. Diesen Operator tauchte in der letzten Woche bereits in der Tabelle im Abschnitt “Operatorpräzedenz” auf. In die eckigen Klammern wird der Index oder, bei benannten Vektoren, der Name des ausgewählten Elements geschrieben. Als Beispiel für den Zugriff über den Index sehen wir uns einige Zugriffsoperationen auf den Vektor fruechte an, den wir hier erneut erstellen:

fruechte <- c("Apfel", "Banane", "Erdbeere", "Apfel")

# Zugriff auf das erste Element des Vektors leckere_fruechte über den Index
fruechte[1]

#> [1] "Apfel"

# Zugriff auf Elemente 1-3
fruechte[1:3]

#> [1] "Apfel"    "Banane"   "Erdbeere"

# Zugriff auf Elemente 1 und 3
fruechte[c(1,3)]

#> [1] "Apfel"    "Erdbeere"

# Zugriff auf alle Elemente mit dem Wert "Banane"
fruechte[fruechte == "Banane"]

#> [1] "Banane"

Die Zugriffsoperation fruechte[fruechte == "Banane"] bedarf vielleicht einer kurzen Erläuterung. Wie funktioniert diese Operation? Warum werden nur die Elemente ausgegeben, deren Wert “Banane” ist?

Zunächst wird der Ausdruck in den eckigen Klammern evaluiert, fruechte == "Banane". Dabei wird ein Mechanismus aktiviert, der sich Vektorisierung nennt (s. nächster Abschnitt): Beim Auswerten des Ausdrucks fruechte == "Banane" wird einzeln für jedes Element überprüft, ob dieses Element dem Wert “Banane” entspricht. Der Ausdruck wird also zu einem Vektor aus Wahrheitswerten ausgewertet wird und nicht zu einem einzelnen Wahrheitswert wie in den Beispielen aus der letzten Woche. Wenn im Vektor fruechte der Wert “Banane” steht, steht in diesem Vektor TRUE und sonst FALSE. Danach wird die eigentliche Zugriffsoperation ausgeführt, allerdings mit dem logischen Vektor anstelle der Indizes: fruechte[c(FALSE, TRUE, FALSE, FALSE)]. Bei einer solchen Zugriffsoperation werden alle Elemente ausgegeben, für die in dem logischen Vektor TRUE steht. Eine Zugriffsoperation der Art fruechte == "Banane", wird deswegen auch bedingter Zugriff genannt. Anstelle des logischen Operators == kann hier auch ein anderer logischer Operator oder ein Vergleichsoperator stehen.

Elemente in einem Vektor können auch ausgetauscht, hinzugefügt oder entfernt werden:

# Element an Indexposition 1 austauschen
fruechte[1] <- "Orange"

# Neues Element an Indexposition 5 hinzufügen
fruechte[5] <- "Birne"

# Neues Element am Ende des Vektors hinzufügen
fruechte <- c(fruechte, "Melone")

# Neues Element am Anfang des Vektors hinzufügen
fruechte <- c("Traube", fruechte)

# Element an Indexposition 1 entfernen
fruechte[-1]

#> [1] "Orange"   "Banane"   "Erdbeere" "Apfel"    "Birne"    "Melone"

Elemente können auch direkt einer neuen Variable zugewiesen werden:

erste_frucht <- fruechte[1] 
print(erste_frucht)

#> [1] "Traube"

Um sich die Anzahl der Werte in einem Vektor (also dessen “Länge”) ausgeben zu lassen, kann die Funktion length() verwendet werden:

length(c("Apfel", "Banane", "Erdbeere", "Apfel"))

#> [1] 4

Die Funktion length() kann mit der Funktion unique() kombiniert werden, um die Anzahl der einzigartigen Werte in einem Vektor auszugeben:

length(unique(c("Apfel", "Banane", "Erdbeere", "Apfel")))

#> [1] 3

Um auf die Elemente eines benannten Vektors zuzugreifen, kann entweder der Index oder der Name des Elements verwendet werden:

einkauf <- c("Apfel"=4, "Banane"=3, "Erdbeere"=20, "Apfel"=5)

# Zugriff auf das Element mit dem Namen "Erdbeere": Hier müssen die Anführungszeichen wieder explizit angegeben werden (zur Erinnerung: Schlüssel sind immer character!)
einkauf["Erdbeere"]

#> Erdbeere 
#>       20

# Zugriff auf den Wert ohne den Namen
einkauf[["Erdbeere"]]

#> [1] 20

# Zugriff auf alle Elemente mit dem Namen "Apfel": 
einkauf["Apfel"]

#> Apfel 
#>     4

# Zugriff auf mehrere Elemente
einkauf[c("Apfel", "Erdbeere")]

#>    Apfel Erdbeere 
#>        4       20

# Wert (!) des Elements mit dem Namen "Banane" austauschen
einkauf["Banane"] <- 5

# Neues Element mit dem Namen "Birne" hinzufügen
einkauf["Birne"] <- 3

# Neues Element am Ende des Vektors hinzufügen
einkauf <- c(einkauf, Melone=1)

# Neues Element am Anfang des Vektors hinzufügen
einkauf <- c(Traube=12, einkauf)

# Element mit dem Namen "Birne" entfernen: 
einkauf <- einkauf[!(names(einkauf) == "Birne")]
einkauf

#>   Traube    Apfel   Banane Erdbeere    Apfel   Melone 
#>       12        4        5       20        5        1

Um nur auf die Level, also die verschiedenen Arten von Werten in einem Faktor zuzugreifen, wird die Funktion levels() verwendet:

fruechte <- c("Apfel", "Banane", "Erdbeere", "Apfel")
fruechte_fct <- factor(fruechte)
levels(fruechte_fct)

#> [1] "Apfel"    "Banane"   "Erdbeere"

Wir haben bereits gesehen, dass die Funktion length() mit der Funktion unique() kombiniert werden kann, um sich die Anzahl der einzigartigen Werte in einem Vektor ausgeben zu lassen. Aber wenn man herausfinden möchte, wie oft jeder Wert jeweils vorkommt, dann ist das mithilfe der unique() Funktion kompliziert:

# Diesen Code müsst ihr nicht verstehen, er dient nur, um die Komplexität zu illustrieren
haeufigkeiten <- sapply(unique(fruechte), function(x) sum(fruechte == x))
haeufigkeiten

#>    Apfel   Banane Erdbeere 
#>        2        1        1

Mithilfe von Faktoren können wir viel einfacher herausfinden, wie oft jeder Wert vorkommt, und zwar mithilfe der Funktion table():

table(factor(fruechte))

#> 
#>    Apfel   Banane Erdbeere 
#>        2        1        1

Tatsächlich wandelt die Funktion table() automatisch den Vektor in einen Faktor um. Wenn wir herausfinden wollen, wie oft jeder Wert in einem Vektor vorkommt, dann brauchen wir also nicht unbedingt erst den Vektor in einen Faktor umwandeln. Wir können die table()-Funktion direkt auf den Vektor anwenden:

table(fruechte)

#> fruechte
#>    Apfel   Banane Erdbeere 
#>        2        1        1

Wie wir gesehen haben, greift die Funktion table() unter der Motorhaube auf Faktoren zurück und wandeln einen Vektor automatisch in einen Faktor um.

Verständnisfragen:

Wie viele Elemente hat der Vektor fruechte?
Wie kann das Element "Orange" aus dem Vektor fruechte entfernt werden? An welcher Indexposition steht es jetzt?
Sind einzelne Zahlen oder Zeichenketten in R auch Datenstrukturen? Wenn ja, welche?
Zu welchem Wahrheitswert wird der Ausdruck c(2) == 2 evaluiert? Warum?
Wie kann auf alle Elemente mit dem Wert 3 im Vektor einkauf zugegriffen werden?

2.2.6 Vektorisierung

Im Abschnitt “Operationen auf Vektoren” habt ihr bereits gesehen, dass die bereits bekannten Operatoren wie ==, > oder + auch auf Vektoren angewendet werden können. Wenn Operatoren auf Vektoren angewandt werden, wird die Operation automatisch elementweise auf jedes Element des Vektors angewandt. Dieser Mechanismus nennt sich Vektorisierung. Wir werden in der Sitzung zu Funktionen noch einmal darauf zurückkommen. Wichtig ist dabei zu beachten, dass beide Vektoren die gleiche Länge haben müssen.

Auf Vektoren vom Typ numeric oder integer (also Vektoren, deren Elemente alle numerics oder integers sind) können die arithmetischen Operatoren angewandt werden, zum Beispiel:

vec_1 <- c(1, 2, 3)
vec_2 <- c(3, 5, 6)
vec_1 + vec_2

#> [1] 4 7 9

Wird ein Vektor nicht mit einem anderen Vektor, sondern mit einem einzelnen Wert addiert (oder subtrahiert, dividiert, … ), dann wird jedes Element des Vektors mit diesem Wert verrechnet:

vec_1 + 5

#> [1] 6 7 8

Daneben können auch Vergleichsoperatoren und logische Operatoren auf Vektoren angewandt werden, und es können sogar zwei Vektoren elementweise verglichen werden:

vec_1 == vec_2

#> [1] FALSE FALSE FALSE

vec_1 < vec_2

#> [1] TRUE TRUE TRUE

vec_1 < 3

#> [1]  TRUE  TRUE FALSE

In der letzten Sitzung haben wir bereits den Unterschied zwischen dem “elementweisen” Operatoren & und | und den Operatoren && und || angeschnitten. Das Verhalten war bei der Auswertung einfacher Ausdrücke mit einzelnen Werten nicht bemerkbar, aber es wird relevant, wenn die Operatoren auf Vektoren anstelle von einzelnen Werten angewandt werden:

zahlen <- 1:5
zahlen > 2 & zahlen < 4

#> [1] FALSE FALSE  TRUE FALSE FALSE

zahlen > 2 && zahlen < 4

#> Error in zahlen > 2 && zahlen < 4: 'length = 5' in coercion to 'logical(1)'

Verständnisfragen:

Warum wird der Ausdruck zahlen > 2 & zahlen < 4 zu FALSE FALSE TRUE FALSE FALSE evaluiert?
Welche Datenstruktur wird ausgegeben, wenn der Ausdruck evaluiert wird?
Was bedeutet die Fehlermeldung bei der Auswertung des Ausdrucks zahlen > 2 && zahlen < 4?

2.3 Listen

Listen enthalten wie Vektoren eine Sequenz von Werten. Im Abschnitt zu Vektoren haben wir bereits gelernt, dass diese Werte auch Elemente genannt werden. Genau wie bei Vektoren können sich Werte in einer Liste wiederholen. Die Elemente einer Liste sind ebenfalls geordnet, das heißt jedes Element hat einen Index, genau wie bei Vektoren. Ähnlich wie bei benannten Vektoren kann man den Elementen einer Liste außerdem einen Namen (wird manchmal auch Schlüssel genannt) zuordnen, über den auf den Wert zugegriffen werden kann. Anders als bei Vektoren können die Elemente einer Liste aber verschiedene Datentypen haben.

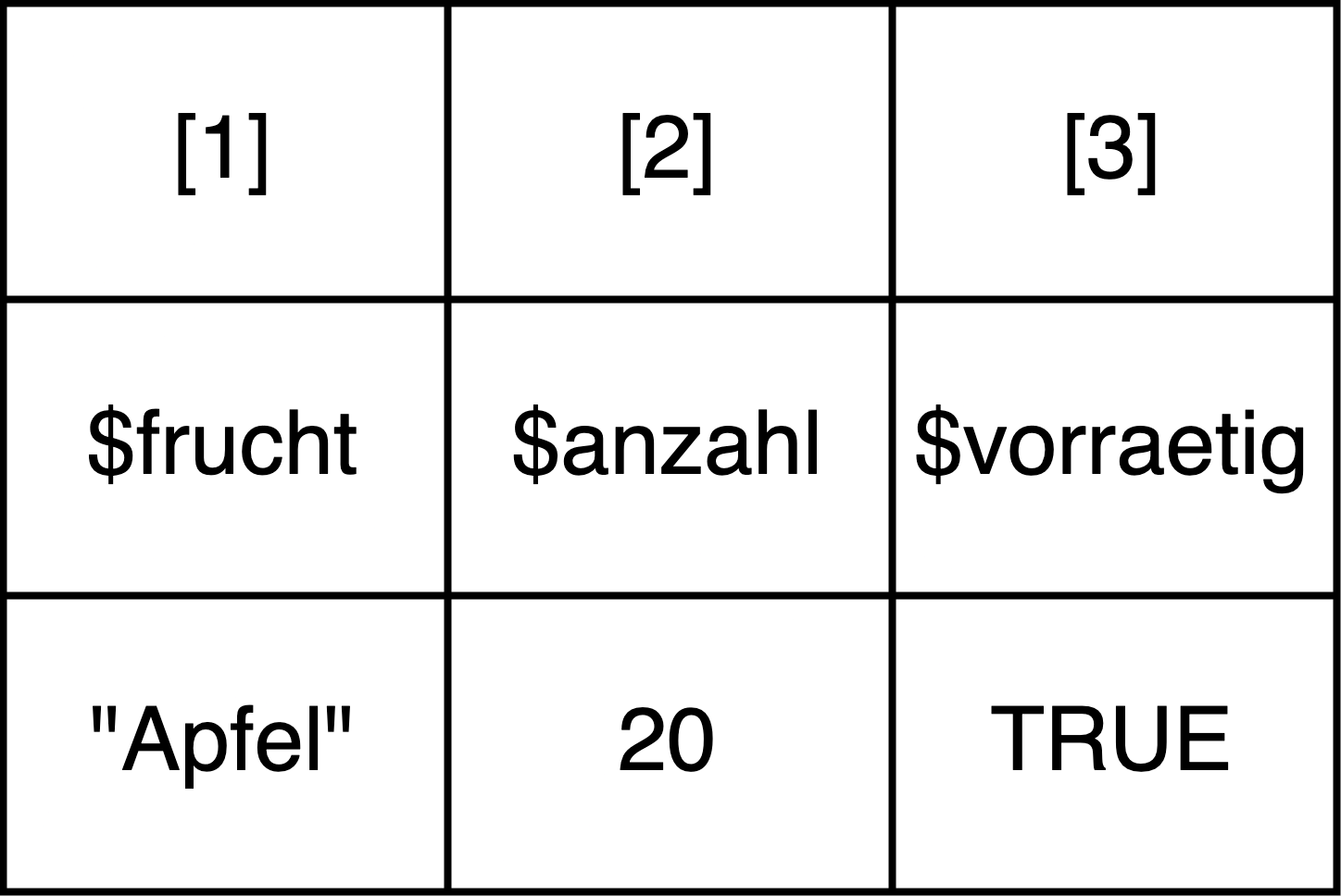
2.3.1 Listen erstellen

Listen werden mithilfe der Funktion list() erstellt. Genau wie bei benannten Vektoren müssen die Namen oder Schlüssel der Werte Zeichenketten sein. Wenn keine Anführungszeichen angegeben werden, erkennt R auch hier automatisch, dass eine Zeichenkette gemeint ist.

# Liste erstellen 
einkauf_liste <- list(frucht="Apfel", anzahl=20, vorraetig=TRUE)

# Liste ausgeben 
print(einkauf_liste)

#> $frucht
#> [1] "Apfel"
#> 
#> $anzahl
#> [1] 20
#> 
#> $vorraetig
#> [1] TRUE

Die einzelnen Elemente müssen dabei nicht unbedingt benannt werden, das heißt, der Code oben könnte genausogut so aussehen:

list("Apfel", 20, TRUE)

#> [[1]]
#> [1] "Apfel"
#> 
#> [[2]]
#> [1] 20
#> 
#> [[3]]
#> [1] TRUE

Die Elemente einer Liste können auch Vektoren oder selbst Listen sein. Im ersten Fall wird die Liste dann “Liste von Vektoren” und im letzteren Fall “Liste von Listen” genannt. Ein allgemeiner Begriff für solche Listen ist “verschachtelte Liste”.

# Liste von Vektoren erstellen: 
liste_von_vektoren <- list(frucht = c("Apfel", "Erdbeere", "Banane"),
                           anzahl = c(20, 32, 0),
                           vorraetig = c(TRUE, TRUE, FALSE)
              )
print(liste_von_vektoren)

#> $frucht
#> [1] "Apfel"    "Erdbeere" "Banane"  
#> 
#> $anzahl
#> [1] 20 32  0
#> 
#> $vorraetig
#> [1]  TRUE  TRUE FALSE

# Liste von Listen erstellen: 
liste_von_listen <- list(Apfel = list(20, FALSE),
                         Erdbeere = list(32, FALSE),
                         Banane = list(0, TRUE)
)
print(liste_von_listen)

#> $Apfel
#> $Apfel[[1]]
#> [1] 20
#> 
#> $Apfel[[2]]
#> [1] FALSE
#> 
#> 
#> $Erdbeere
#> $Erdbeere[[1]]
#> [1] 32
#> 
#> $Erdbeere[[2]]
#> [1] FALSE
#> 
#> 
#> $Banane
#> $Banane[[1]]
#> [1] 0
#> 
#> $Banane[[2]]
#> [1] TRUE

Achtung: In der Liste liste_von_vektoren sind alle Vektoren gleich lang und beziehen sich aufeinander: Von der Frucht Apfel sind noch 20 Stück da, sodass Äpfel vorrätig sind. Dies muss aber nicht unbedingt der Fall sein! Die Elemente einer verschachtelten Liste können unterschiedlich lang sein und müssen sich nicht unbedingt aufeinander beziehen.

Schematisch sieht eine Liste von Vektoren (hier mit Vektoren derselben Länge) in etwa so aus:

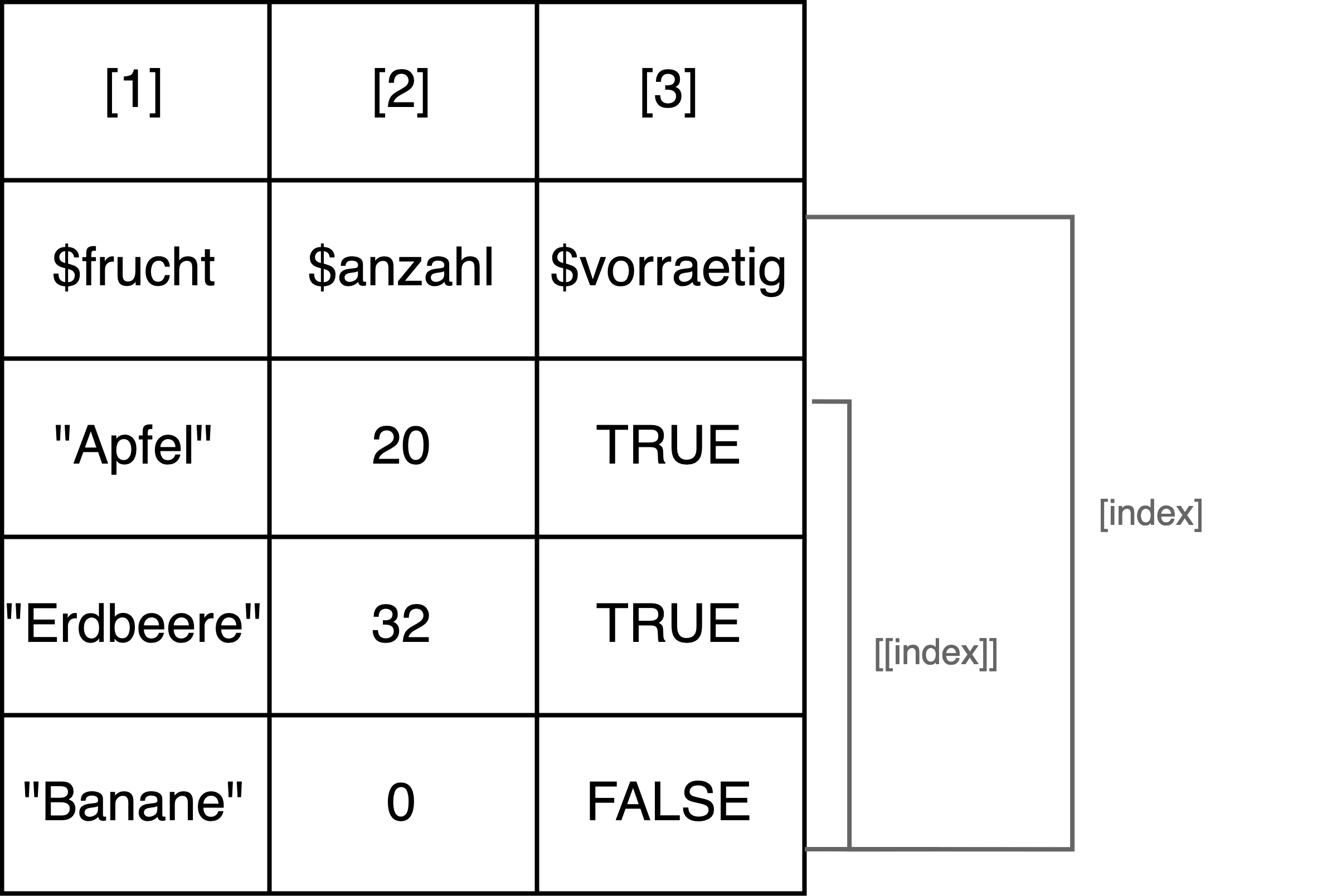
Das Bild illustriert auch, wie auf die Elemente in einer Liste von Vektoren zugegriffen werden kann. Der Zugriff auf Elemente in einer Liste ist nämlich etwas komplizierter als bei einem Vektor. Darum geht es im folgenden Abschnitt.

2.3.2 Operationen auf Listen

Auf Elemente und ihre Namen über den Index zugreifen:

einkauf_liste[1]

#> $frucht
#> [1] "Apfel"

Auf Elemente ohne Namen über den Index zugreifen:

einkauf_liste[[1]]

#> [1] "Apfel"

Auf Elemente über den Namen (Schlüssel) zugreifen:

# Option 1 
einkauf_liste$frucht

#> [1] "Apfel"

# Option 2
einkauf_liste[["frucht"]]

#> [1] "Apfel"

Auf das erste Element des ersten Vektors in einer Liste von Vektoren über den Index zugreifen:

liste_von_vektoren[[1]][1]

#> [1] "Apfel"

Auf das erste Element des ersten Vektors in einer Liste von Vektoren über den Schlüssel zugreifen

# Option 1
liste_von_vektoren[["frucht"]][1]

#> [1] "Apfel"

# Option 2
liste_von_vektoren$frucht[1]

#> [1] "Apfel"

Listen kombinieren mit der Funktion c():

einkauf_bananen <- list(frucht="Banane", anzahl=0, vorraetig=FALSE)
einkauf_gesamt <- c(einkauf_liste, einkauf_bananen)

Verständnisfragen:

Um welche Datenstruktur handelt es sich bei dem Objekt einkauf_gesamt?
Was ist der Datentyp der Elemente des Objekts einkauf_gesamt?
Was ist der Unterschied zwischen Listen und Named Vectors?

Sehr anschaulich illustriert dieser Abschnitt in Hadley Wickham’s Lehrbuch “Advanced R” den Unterschied zwischen dem Zugriff mit einfachen und mit doppelten eckigen Klammern:

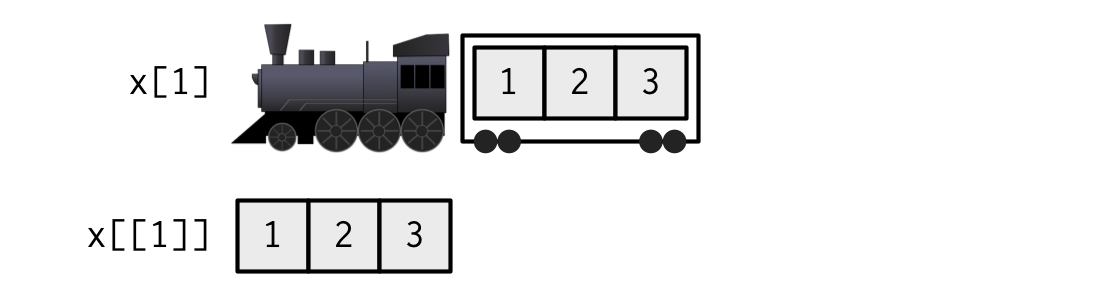
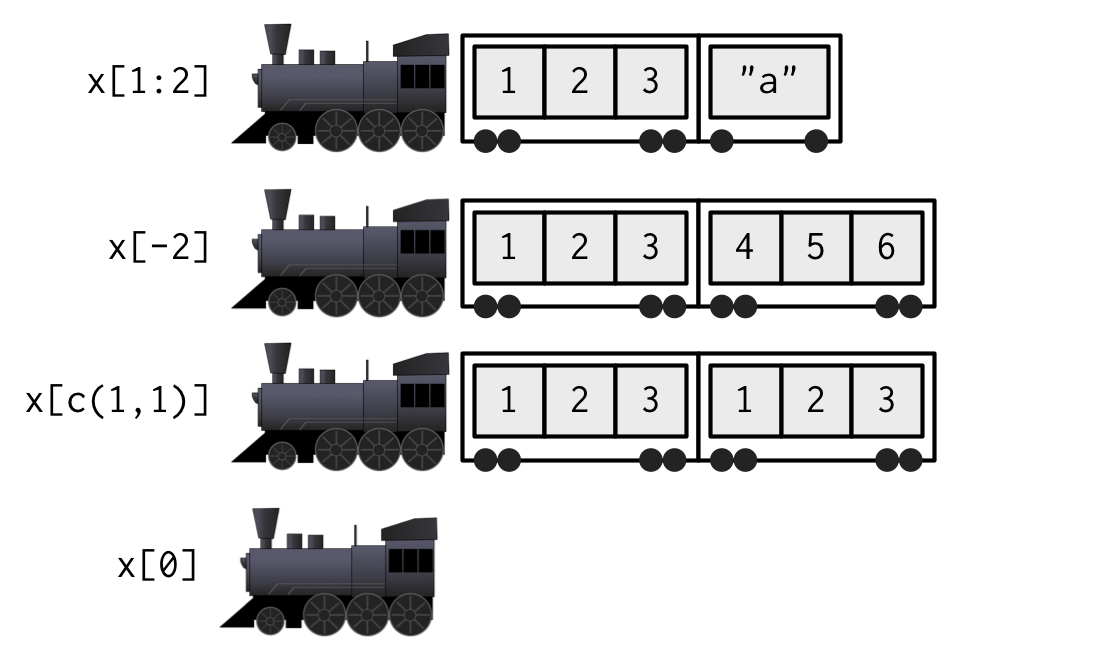
Figure 2.1: Quelle: Hadley Wickham (2019), https://adv-r.hadley.nz/subsetting.html#subset-single

Im letzten Beispiel haben wir die bereits bekannte Funktion c() verwendet, um zwei Listen in eine neue Liste einkauf_gesamt zu kombinieren. Das heißt: Wenn wir die Funktion c() verwenden, um zwei Listen zu kombinieren, dann kommt auch eine Liste dabei raus. Man kann mit der Funktion c() aber keine Listen aus einzelnen Werten erstellen:

# Mit der Funktion c() kann man KEINE Liste erstellen
einkauf_bananen <- c(frucht="Banane", anzahl=0, vorraetig=FALSE)
typeof(einkauf_bananen)

#> [1] "character"

2.4 Auf einen Blick: Vektoren vs benannte Vektoren vs Faktoren vs Listen

In diesem Abschnitt werden die Unterschiede zwischen einfachen Vektoren, benannten Vektoren, Faktoren und Listen anhand eines Beispiels illustriert. Das Beispiel illustriert, wie Daten zu Wetterbedingungen für jeden Monat eines Jahres mithilfe der verschiedenen Datenstrukturen organisiert werden können.

# Vektor: Ein einfacher Vektor, der die Wetterbedingungen für jeden Monat eines Jahres speichert.
weather_conditions <- c("sonnig", "bewölkt", "sonnig", "regnerisch", "bewölkt", "sonnig",
                        "regnerisch", "bewölkt", "bewölkt", "sonnig", "bewölkt", "regnerisch")
avg_rainfall <- c(50, 40, 45, 60, 55, 70, 80, 75, 70, 65, 55, 50)
print(weather_conditions)

#>  [1] "sonnig"     "bewölkt"    "sonnig"     "regnerisch" "bewölkt"   
#>  [6] "sonnig"     "regnerisch" "bewölkt"    "bewölkt"    "sonnig"    
#> [11] "bewölkt"    "regnerisch"

print(avg_rainfall)

#>  [1] 50 40 45 60 55 70 80 75 70 65 55 50

# Named Vector: Ein benannter Vektor, der die Wetterbedingungen für jeden Monat eines Jahres speichert und Monatsnamen als Namen für jedes Element verwendet. 
weather_conditions_named <- c(Jan="sonnig", Feb="bewölkt", Mar="sonnig", Apr="regnerisch",
                              Mai="bewölkt", Jun="sonnig", Jul="regnerisch", Aug="bewölkt",
                              Sep="bewölkt", Okt="sonnig", Nov="bewölkt", Dez="regnerisch")
print(weather_conditions_named)

#>          Jan          Feb          Mar          Apr          Mai          Jun 
#>     "sonnig"    "bewölkt"     "sonnig" "regnerisch"    "bewölkt"     "sonnig" 
#>          Jul          Aug          Sep          Okt          Nov          Dez 
#> "regnerisch"    "bewölkt"    "bewölkt"     "sonnig"    "bewölkt" "regnerisch"

# Faktor: Häufigkeitsverteilung der Wetterbedingungen
# Konvertieren des Vektors in einen Faktor mit benannten Ebenen
weather_factor <- factor(weather_conditions, levels=c("sonnig", "bewölkt", "regnerisch"), ordered=TRUE)
# Häufigkeitsverteilung der Wetterbedingungen
weather_table <- table(weather_factor)
# Ergebnis anzeigen
print(weather_table)

#> weather_factor
#>     sonnig    bewölkt regnerisch 
#>          4          5          3

# Liste: Eine Liste, die Informationen über das Wetter für jeden Monat des Jahres enthält. 
# Jedes Element der Liste ist ein eigenes Objekt, in diesem Fall ein Vektor. 
weather_list <- list(Condition=weather_conditions, 
                     Rainfall=avg_rainfall,
                     Month=c("Januar", "Februar", "Maerz", "April", "Mai", "Juni", "Juli", "August", "September", "Oktober", "November", "Dezember"))
print(weather_list)

#> $Condition
#>  [1] "sonnig"     "bewölkt"    "sonnig"     "regnerisch" "bewölkt"   
#>  [6] "sonnig"     "regnerisch" "bewölkt"    "bewölkt"    "sonnig"    
#> [11] "bewölkt"    "regnerisch"
#> 
#> $Rainfall
#>  [1] 50 40 45 60 55 70 80 75 70 65 55 50
#> 
#> $Month
#>  [1] "Januar"    "Februar"   "Maerz"     "April"     "Mai"       "Juni"     
#>  [7] "Juli"      "August"    "September" "Oktober"   "November"  "Dezember"

# Andere Darstellungsform als Liste von Listen
weather_list <- list(Januar=list(50, "sonnig"),
                     Februar=list(40, "bewölkt"), 
                     Maerz=list(45, "sonnig"), 
                     April=list(60, "regnerisch"),
                     Mai=list(55, "bewölkt"),
                     Juni=list(70, "sonnig"),
                     Juli=list(80, "regnerisch"),
                     August=list(75, "bewölkt"),
                     September=list(70, "bewölkt"),
                     Oktober=list(65, "sonnig"),
                     November=list(55, "bewölkt"),
                     Dezember=list(50, "regnerisch")
)
print(weather_list)

#> $Januar
#> $Januar[[1]]
#> [1] 50
#> 
#> $Januar[[2]]
#> [1] "sonnig"
#> 
#> 
#> $Februar
#> $Februar[[1]]
#> [1] 40
#> 
#> $Februar[[2]]
#> [1] "bewölkt"
#> 
#> 
#> $Maerz
#> $Maerz[[1]]
#> [1] 45
#> 
#> $Maerz[[2]]
#> [1] "sonnig"
#> 
#> 
#> $April
#> $April[[1]]
#> [1] 60
#> 
#> $April[[2]]
#> [1] "regnerisch"
#> 
#> 
#> $Mai
#> $Mai[[1]]
#> [1] 55
#> 
#> $Mai[[2]]
#> [1] "bewölkt"
#> 
#> 
#> $Juni
#> $Juni[[1]]
#> [1] 70
#> 
#> $Juni[[2]]
#> [1] "sonnig"
#> 
#> 
#> $Juli
#> $Juli[[1]]
#> [1] 80
#> 
#> $Juli[[2]]
#> [1] "regnerisch"
#> 
#> 
#> $August
#> $August[[1]]
#> [1] 75
#> 
#> $August[[2]]
#> [1] "bewölkt"
#> 
#> 
#> $September
#> $September[[1]]
#> [1] 70
#> 
#> $September[[2]]
#> [1] "bewölkt"
#> 
#> 
#> $Oktober
#> $Oktober[[1]]
#> [1] 65
#> 
#> $Oktober[[2]]
#> [1] "sonnig"
#> 
#> 
#> $November
#> $November[[1]]
#> [1] 55
#> 
#> $November[[2]]
#> [1] "bewölkt"
#> 
#> 
#> $Dezember
#> $Dezember[[1]]
#> [1] 50
#> 
#> $Dezember[[2]]
#> [1] "regnerisch"

2.5 Matrizen

Eine Matrix ist in R im Grunde eine Kombination mehrerer Vektoren in Spalten und Zeilen. Formell ausgedrückt: In einer Matrix kann jede Spalte und jede Zeile als Vektor aufgefasst werden. Das heißt, dass jedes Element in einer Matrix denselben Datentyp hat, eben genau wie bei Vektoren. Wenn beispielsweise alle Elemente den Typ character haben, spricht man auch von einer character-Matrix. Zusätzlich haben Matrizen eine Dimension, die mithilfe der Funktion dim() abgefragt werden kann. Die Dimension einer Matrix ist die Anzahl ihrer Zeilen und Spalten. Die Matrix unten hat beispielsweise die Dimension 2x3: Sie hat zwei Zeilen und drei Spalten.

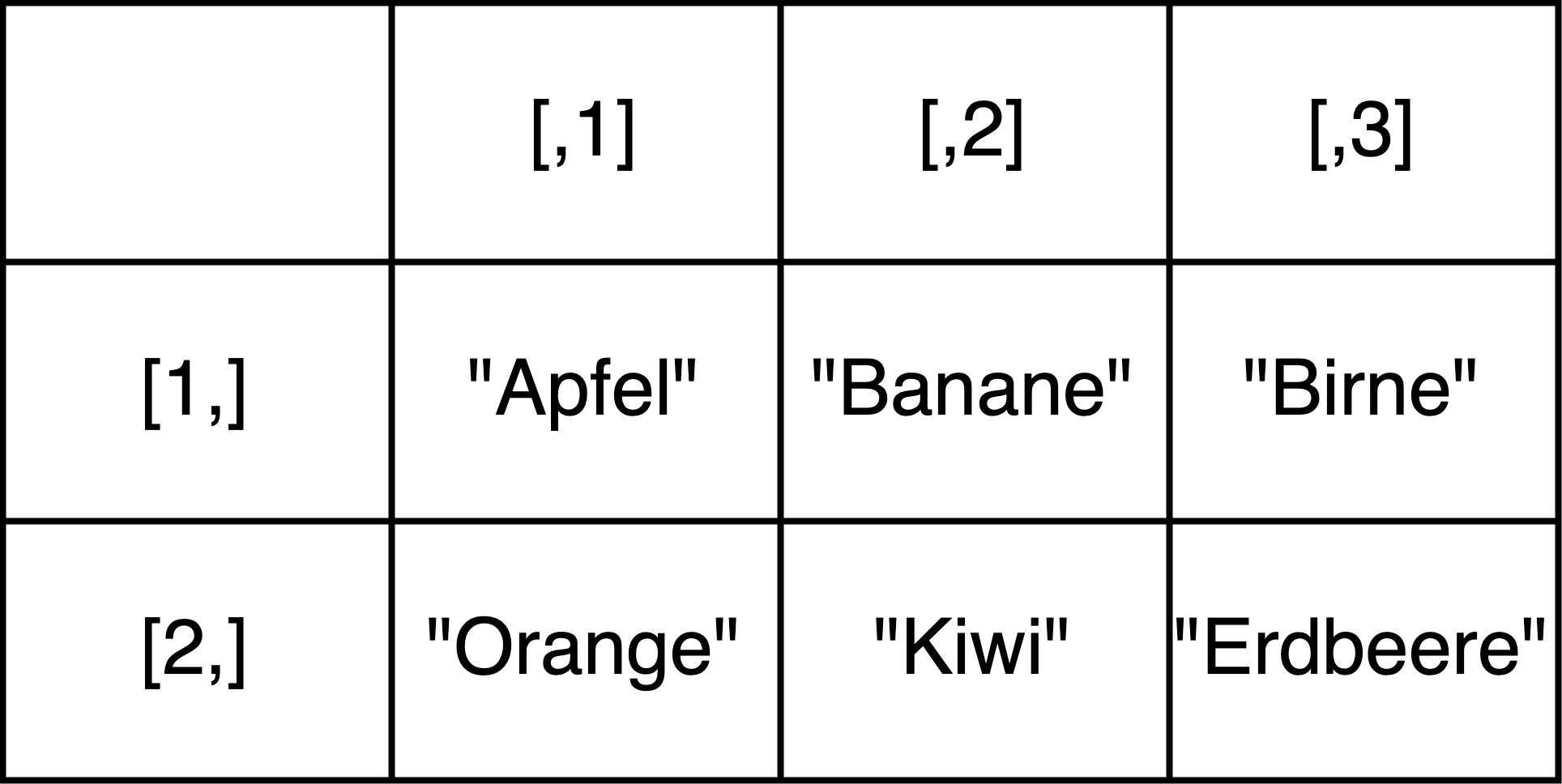
2.5.1 Matrizen erstellen

Da Matrizen aus Vektoren bestehen, können Matrizen erstellt werden, indem mehrere Vektoren kombiniert werden, oder, indem ein einzelner Vektor in verschiedene Spalten aufgeteilt wird. Dabei wird bei der Erstellung der Matrix mithilfe dem Zusatz ncol festgelegt, in wie viele Spalten die Elemente des Vektors organisiert werden sollen.

Wir betrachten zunächst ein ganz simples Beispiel:

# Matrix aus einem einzigen Vektor erstellen mit der Funktion matrix() 
fruechte <- matrix(c("Apfel", "Orange", "Banane", "Kiwi", "Birne", "Erdbeere"), ncol = 3)
print(fruechte)

#>      [,1]     [,2]     [,3]      
#> [1,] "Apfel"  "Banane" "Birne"   
#> [2,] "Orange" "Kiwi"   "Erdbeere"

# Dimension einer Matrix ausgeben lassen
dim(fruechte) # Dimension ist 2 x 3

#> [1] 2 3

Die Matrix fruechte ist jedoch nicht sehr informativ. Häufig haben die Spalten und Zeilen einer Matrix eine Bedeutung, sodass es sinnvoll ist, die Zeilen und/oder Spalten zu benennen. Wenn die Matrix wie im Beispiel oben aus einem einzelnen Vektor erstellt wird, können direkt beim Erstellen der Matrix die Zeilen- und Spaltennamen angegeben werden. In unserem Beispiel macht es nicht so viel Sinn, auch den Zeilen eine Bedeutung zu geben. Deswegen verwenden wir in der Funktion list() innerhalb der Funktion matrix() hier den Wert NULL (siehe dazu den Abschnitt “Fehlende und ungültige Werte in Datenstrukturen”). Wenn Zeilennamen festgelegt werden sollen, kann NULL einfach durch einen Vektor mit den Zeilennamen ausgetauscht werden. Beachtet, dass es einen Unterschied macht, ob die Elemente der Liste einen Namen haben oder nicht:

# Matrix erstellen und direkt Namen für die Spalten festlegen 
# Achtung: die Dimension ist jetzt 3 x 2 !

matrix(c("Apfel", "Orange", "Banane", "Kiwi", "Birne", "Erdbeere"), 
       ncol = 2, 
       dimnames = list(NULL,
                      c("nicht_vorraetig", "vorraetig")))

#>      nicht_vorraetig vorraetig 
#> [1,] "Apfel"         "Kiwi"    
#> [2,] "Orange"        "Birne"   
#> [3,] "Banane"        "Erdbeere"

# Matrix erstellen, Namen für einzelne Spalten festlegen, und Spalten insgesamt benennen
matrix(c("Apfel", "Orange", "Banane", "Kiwi", "Birne", "Erdbeere"), 
       ncol = 2, 
       dimnames = list(NULL,
                      "Vorratsstatus" = c("nicht_vorraetig", "vorraetig")))

#>       Vorratsstatus
#>        nicht_vorraetig vorraetig 
#>   [1,] "Apfel"         "Kiwi"    
#>   [2,] "Orange"        "Birne"   
#>   [3,] "Banane"        "Erdbeere"

Wenn Matrizen aus mehreren Vektoren erstellt werden, sind die Spalten- bzw. Zeilennamen automatisch die Namen der Vektoren, aus denen die Matrix erstellt wurde. Um Matrizen aus bereits existierenden Vektoren zu erstellen, kann entweder die Funktion rbind() oder die Funktion cbind() verwendet werden. rbind() fügt die Vektoren als Zeilen, also übereinander, zusammen. cbind() fügt die Vektoren als Spalten, also nebeneinander, zusammen.

# Matrix zeilenweise erstellen mit der Funktion rbind()
nicht_vorraetig <- c("Banane", "Orange", "Birne")
vorraetig <- c("Apfel", "Erbeere", "Kiwi") 
fruechte_einkauf <- rbind(nicht_vorraetig, vorraetig)
fruechte_einkauf

#>                 [,1]     [,2]      [,3]   
#> nicht_vorraetig "Banane" "Orange"  "Birne"
#> vorraetig       "Apfel"  "Erbeere" "Kiwi"

# Matrix spaltenweise erstellen mit der Funktion cbind()
nicht_vorraetig <- c("Banane", "Orange", "Birne")
vorraetig <- c("Apfel", "Erbeere", "Kiwi") 
fruechte_einkauf <- cbind(nicht_vorraetig, vorraetig)
fruechte_einkauf

#>      nicht_vorraetig vorraetig
#> [1,] "Banane"        "Apfel"  
#> [2,] "Orange"        "Erbeere"
#> [3,] "Birne"         "Kiwi"

Matrizen können auch aus anderen bereits existierenden Matrizen erstellt werden. Hierzu könen ebenfalls die Funktionen rbind() und cbind() verwendet werden:

# Matrizen zeilenweise kombinieren
mat_3 <- rbind(nicht_vorraetig, vorraetig)
mat_3

#>                 [,1]     [,2]      [,3]   
#> nicht_vorraetig "Banane" "Orange"  "Birne"
#> vorraetig       "Apfel"  "Erbeere" "Kiwi"

# Matrizen spaltenweise kombinieren
mat_4 <- cbind(nicht_vorraetig, vorraetig)
mat_4

#>      nicht_vorraetig vorraetig
#> [1,] "Banane"        "Apfel"  
#> [2,] "Orange"        "Erbeere"
#> [3,] "Birne"         "Kiwi"

Matrizen können auch in Dataframes umgewandelt werden und umgekehrt. Das behandeln wir im Abschnitt “Dataframes”.

2.5.2 Operationen auf Matrizen

Zugriff auf eine Zeile und Zeilen (um)benennen:

# Zugriff auf Zeile 1
fruechte[1, ]

#> [1] "Apfel"  "Banane" "Birne"

# Zeilen nachträglich (um)benennen
rownames(fruechte_einkauf) <- c("kuehlschrank", "vorratskammer", "regal")
fruechte_einkauf

#>               nicht_vorraetig vorraetig
#> kuehlschrank  "Banane"        "Apfel"  
#> vorratskammer "Orange"        "Erbeere"
#> regal         "Birne"         "Kiwi"

# Zugriff auf Zeile mit dem Namen "kuehlschrank"
fruechte_einkauf["kuehlschrank", ]

#> nicht_vorraetig       vorraetig 
#>        "Banane"         "Apfel"

Zugriff auf eine Spalte und Spalten (um)benennen:

# Zugriff auf Spalte mit Index 1
fruechte[, 1]

#> [1] "Apfel"  "Orange"

# Zugriff auf Spalte mit dem Namen "vorraetig"
fruechte_einkauf[, "vorraetig"]

#>  kuehlschrank vorratskammer         regal 
#>       "Apfel"     "Erbeere"        "Kiwi"

# Spalten nachträglich (um)benennen
colnames(fruechte_einkauf) <- c("vorhanden", "nicht_vorhanden")

Zugriff auf ein Element:

# Zugriff auf das Element in Zeile 1 und Spalte 2
fruechte[1, 2]

#> [1] "Banane"

Bedingter Zugriff, hier Zugriff auf alle Elemente mit dem Wert “Banane”:

# Zugriff auf alle Elemente mit dem Wert "Banane"
fruechte[fruechte == "Banane"]

#> [1] "Banane"

Da Matrizen aus Vektoren bestehen, können wie auf Vektoren auch auf Matrizen die bereits bekannten Operatoren angewendet werden. Dabei wird wieder der Mechanismus der Vektorisierung aktiviert: Wenn Operatoren auf Matrizen angewandt werden, wird die Operation automatisch elementweise auf jedes Element der Matrix angewandt:

mat_1 <- matrix(c(1, 1, 2, 2), ncol=2)
mat_1 + 2

#>      [,1] [,2]
#> [1,]    3    4
#> [2,]    3    4

# Das geht auch mit zwei Matrizen 
mat_2 <- matrix(c(4, 4, 4, 4), ncol=2)
mat_1 + mat_2

#>      [,1] [,2]
#> [1,]    5    6
#> [2,]    5    6

Matrizen können auch kombiniert werden. Wir haben ja bereits beim Erstellen von Matrizen aus bereits existierenden Vektoren oder Matrizen die Funktionen rbind() und cbind() verwendet:

# Matrizen zeilenweise kombinieren
mat_3 <- rbind(mat_1, mat_2)
mat_3

#>      [,1] [,2]
#> [1,]    1    2
#> [2,]    1    2
#> [3,]    4    4
#> [4,]    4    4

# Matrizen spaltenweise kombinieren
mat_4 <- cbind(mat_1, mat_2)
mat_4

#>      [,1] [,2] [,3] [,4]
#> [1,]    1    2    4    4
#> [2,]    1    2    4    4

Matrizen können aber nicht immer kombiniert werden. Eine Voraussetzung dafür, dass Matrizen kombiniert werden können, ist, dass sie dieselbe Anzahl von Zeilen und Spalten (also dieselbe Dimension) haben. Die beiden Matrizen mat_3 und mat_4 haben beispielsweise umgekehrte Dimensionen: mat_3 ist eine 4x2-Matrix, und mat_4 ist eine 2x4-Matrix. Wenn die beiden Matrizen kombiniert werden sollen, müssen sie erst in dieselbe Form gebracht werden. Das geht ganz einfach mithilfe der Funktion t(). Das t steht dabei für “Transponieren”.

# Matrix mat_3 transponieren
mat_3t <- t(mat_3)
# Matrix mat_4 und transponierte Matrix kombinieren: 
cbind(mat_3t, mat_4)

#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
#> [1,]    1    1    4    4    1    2    4    4
#> [2,]    2    2    4    4    1    2    4    4

Verständnisfragen:

Welche Dimension hat die Matrix fruechte_einkauf?
Welchen Datentyp haben die Elemente der Matrix fruechte_einkauf?
Wie kann man eine Matrix mit fünf Spalten erstellen?

2.6 Arrays

Ein Array ermöglicht, einfach gesagt, mehrere Matrizen von gleicher Größe in einer einzigen Datenstruktur zu “stapeln”, wobei jede Matrix eine eigene “Schicht” oder “Ebene” im Array bildet. Auch Arrays haben eine Dimension, allerdings ist damit in Bezug auf Arrays etwas anderes gemeint als in Bezug auf Matrizen. Während die Dimension einer Matrix die Anzahl ihrer Zeilen und Spalten beschreibt, hat der Dimensionsbegriff bei Arrays eine erweiterte Bedeutung. Bei einem Array bezieht sich die Dimension auf die Anzahl der “Richtungen” oder “Achsen”, in denen die Daten organisiert sind. Dies kann die Anzahl der Zeilen, Spalten, “Schichten” und weiterer Organisationsweisen in höherdimensionalen Arrays umfassen. Jede dieser “Richtungen” hat eine bestimmte Größe, das heißt eine festgelegte Anzahl von Elementen.

Arrays werden mithilfe der Funktion array() erstellt:

# Daten für das Array
fruechte_daten <- c(
    "Apfel", "Orange", "Birne", 
    "Erbeere", "Melone", "Kiwi", 
    "Banane", "Traube", "Apfel", 
    "Papaya", "Quitte", "Mango"
)

# Erstellen eines 3D-Arrays mit 2 Zeilen, 3 Spalten und 2 "Ebenen" (jede Ebene ist eine separate Matrix)
fruechte_array <- array(fruechte_daten, dim = c(2, 3, 2))

# Ausgabe des Arrays
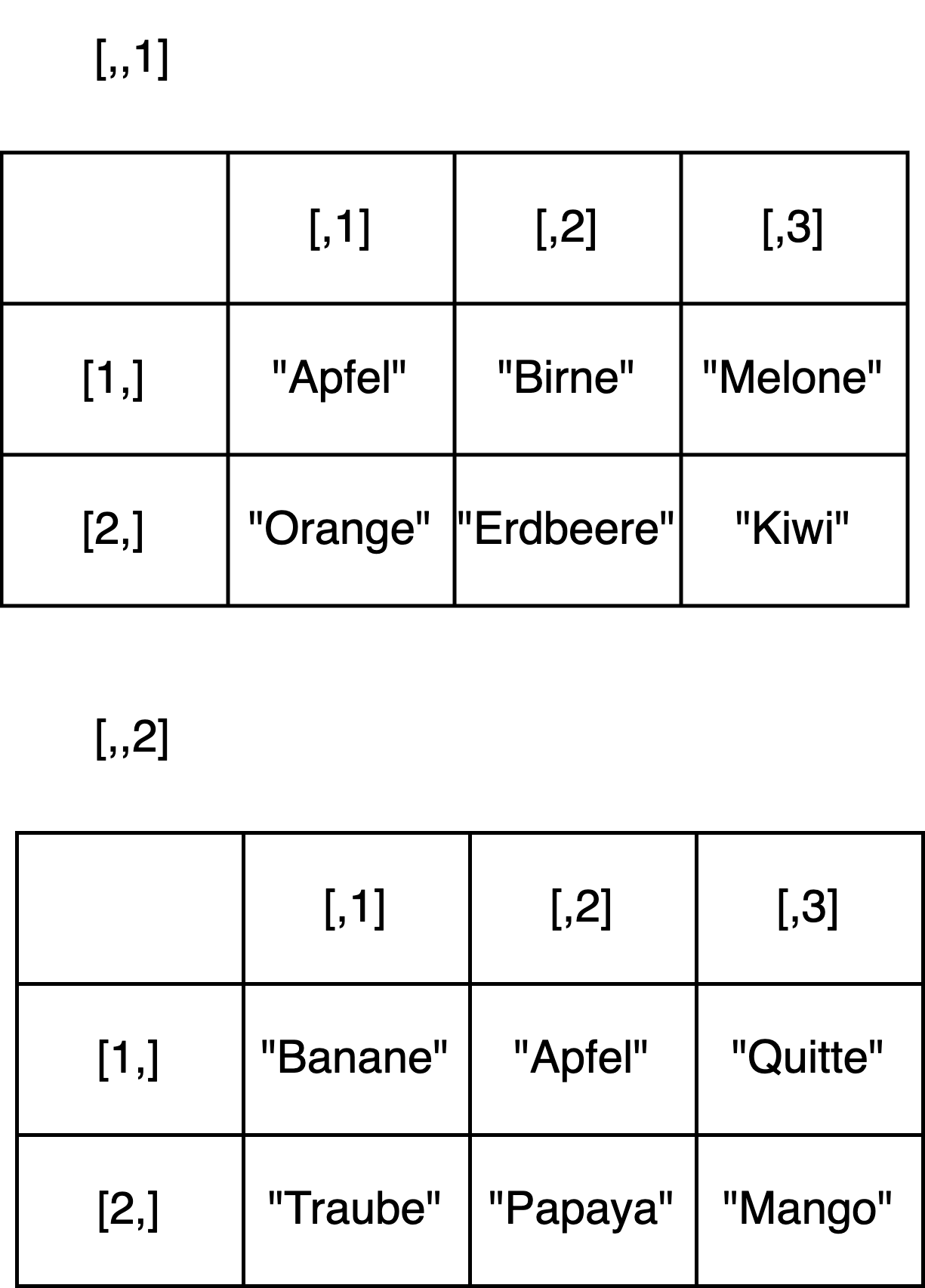
print(fruechte_array)

#> , , 1
#> 
#>      [,1]     [,2]      [,3]    
#> [1,] "Apfel"  "Birne"   "Melone"
#> [2,] "Orange" "Erbeere" "Kiwi"  
#> 
#> , , 2
#> 
#>      [,1]     [,2]     [,3]    
#> [1,] "Banane" "Apfel"  "Quitte"
#> [2,] "Traube" "Papaya" "Mango"

Die Dimension des Arrays fruechte_array lässt sich an der Länge des Vektors dim=c(2, 3, 2) ablesen: Da der Vektor drei Elemente hat, handelt es sich um ein dreidimensionales Array. Das erste Element des Vektors dim legt fest, dass jede Matrix zwei Zeilen hat, das zweite Element legt fest, dass jede Matrix drei Spalten hat, und das dritte Element legt fest, dass es zwei Matrizen gibt.

2.6.1 Operationen auf Arrays

Zugriff auf eine Matrix:

# Zugriff auf die erste Matrix 
fruechte_array[,, 1]

#>      [,1]     [,2]      [,3]    
#> [1,] "Apfel"  "Birne"   "Melone"
#> [2,] "Orange" "Erbeere" "Kiwi"

Zugriff auf eine Spalte einer Matrix:

# Zugriff auf die zweite Spalte der ersten Matrix 
fruechte_array[, 2, 1]

#> [1] "Birne"   "Erbeere"

Zugriff auf ein Element:

# Zugriff auf das Element in der ersten Zeile und zweiten Spalte der ersten Matrix 
fruechte_array[1, 2, 1]

#> [1] "Birne"

Dimensionen benennen:

dimnames(fruechte_array) <- list(
  Vorratsstatus = c("vorraetig", "nicht_vorraetig"),
  Vorratsort = c("kuehlschrank", "vorratskammer", "regal"),
  Haus = c("Wohnhaus", "Ferienhaus")
)
fruechte_array

#> , , Haus = Wohnhaus
#> 
#>                  Vorratsort
#> Vorratsstatus     kuehlschrank vorratskammer regal   
#>   vorraetig       "Apfel"      "Birne"       "Melone"
#>   nicht_vorraetig "Orange"     "Erbeere"     "Kiwi"  
#> 
#> , , Haus = Ferienhaus
#> 
#>                  Vorratsort
#> Vorratsstatus     kuehlschrank vorratskammer regal   
#>   vorraetig       "Banane"     "Apfel"       "Quitte"
#>   nicht_vorraetig "Traube"     "Papaya"      "Mango"

2.7 Dataframes

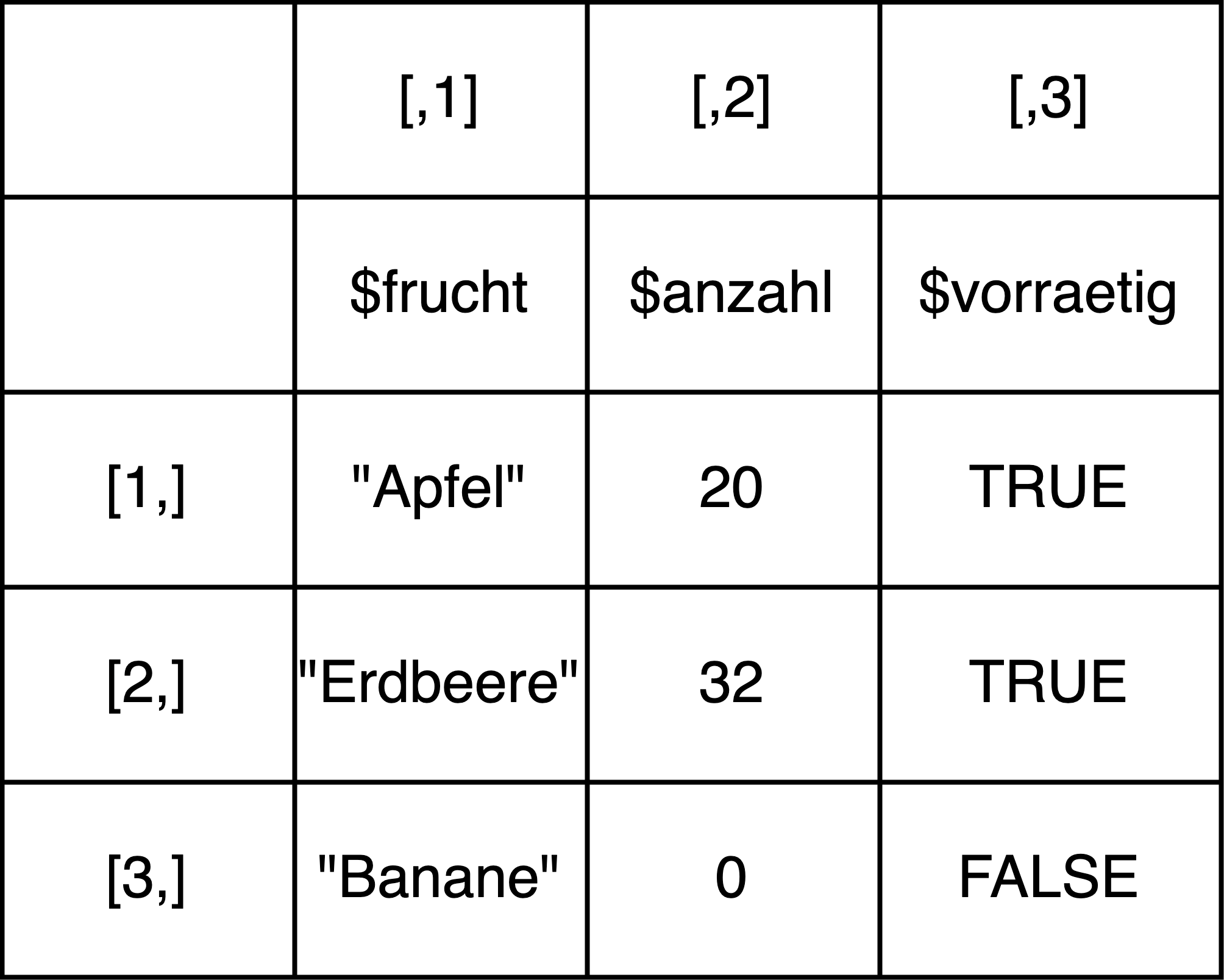
Dataframes werden zur Darstellung tabellarischer Daten verwendet. Sie ähneln auf den ersten Blick Matrizen, jedoch können sie Elemente unterschiedlichen Typs beinhalten: Jede Spalte eines Dataframes ist ein Vektor, aber anders als bei Matrizen können die Zeilen nicht als Vektoren aufgefasst werden, da die Elemente in den verschiedenen Spalten unterschiedliche Datentypen haben können. Genauer gesagt ist ein Dataframe also eigentlich eine Art von Liste von Vektoren, bei der jedes Element, also jeder Vektor, dieselbe Länge haben muss: Eine Liste mit fünf Elementen vom Typ numeric könnte bespielsweise genausogut als Dataframe mit einer Zeile und fünf Spalten dargestellt werden. Eine Liste mit vier Elementen, wobei die Elemente Vektoren mit jeweils zwei Elementen sind, könnte als Dataframe mit zwei Zeilen und vier Spalten dargestellt werden. Anders als bei einer Liste hat in einem Dataframe aber nicht nur jede Spalte, sondern auch jede Zeile einen Index. Darauf kommen wir im Abschnitt “Operationen auf Dataframes” zurück.

2.7.1 Dataframes erstellen

Weil die Spalten eines Dataframes Vektoren sind, kann man Dataframes “spaltenweise” aus Vektoren erstellen. Dazu erstellt man zunächst entweder einen Vektor für jede Spalte und kombiniert diese dann mithilfe der Funktion data.frame() in ein Dataframe-Objekt:

# Dataframe aus Vektoren erstellen: Variante 1 
fruechte <- c("Apfel", "Erdbeere", "Banane")
anzahl <- c(20, 32, 0)
vorraetig <- c(TRUE, TRUE, FALSE)
df <- data.frame(fruechte, anzahl, vorraetig)
print(df)

#>   fruechte anzahl vorraetig
#> 1    Apfel     20      TRUE
#> 2 Erdbeere     32      TRUE
#> 3   Banane      0     FALSE

# Dataframe aus Vektoren erstellen: Variante 2
fruechte_df <- data.frame(frucht = c("Apfel", "Erdbeere", "Banane"),
                          anzahl = c(20, 32, 0),
                          vorraetig = c(TRUE, TRUE, FALSE)
                 )
print(fruechte_df)

#>     frucht anzahl vorraetig
#> 1    Apfel     20      TRUE
#> 2 Erdbeere     32      TRUE
#> 3   Banane      0     FALSE

Dataframes können aber auch aus Listen erstellt werden. Dabei wird zuerst eine Liste erstellt, bei der jedes Element ein Vektor ist und stellt die Liste anschließend mit der Funktion as.data.frame() als Dataframe dar:

# Dataframe aus einer Liste erstellen
liste_von_vektoren <- list(frucht = c("Apfel", "Erdbeere", "Banane"),
                           anzahl = c(20, 32, 0),
                           vorraetig = c(TRUE, TRUE, FALSE)
              )
fruechte_df <- as.data.frame(liste_von_vektoren)
print(fruechte_df)

#>     frucht anzahl vorraetig
#> 1    Apfel     20      TRUE
#> 2 Erdbeere     32      TRUE
#> 3   Banane      0     FALSE

Dataframes können auch aus Matrizen erstellt werden, zum Beispiel aus unserer Matrix fruechte_einkauf:

# Dataframe aus Matrix erstellen 
fruechte_einkauf <- matrix(c("Birne", "Orange", "Banane", "Kiwi", "Apfel", "Erdbeere"), 
                           ncol = 2, 
                           dimnames = list(NULL,
                      c("nicht_vorraetig", "vorraetig")))

fruechte_df <- as.data.frame(fruechte_einkauf)
fruechte_df

#>   nicht_vorraetig vorraetig
#> 1           Birne      Kiwi
#> 2          Orange     Apfel
#> 3          Banane  Erdbeere

Allerdings sind in diesem Fall noch einige Operationen notwendig, um zusätzliche Informationen hinzuzufügen und den Dataframe in die gewünschte Form zu bringen. In unserem Beispiel wäre es sinnvoll, die Früchte in einer Spalte aufzulisten und für den Vorratsstatus wie in den Beispielen zuvor eine eigene Spalte anzulegen:

# Dataframe mithilfe der Funktion stack() umformen 
fruechte_df <- stack(fruechte_df)
fruechte_df

#>     values             ind
#> 1    Birne nicht_vorraetig
#> 2   Orange nicht_vorraetig
#> 3   Banane nicht_vorraetig
#> 4     Kiwi       vorraetig
#> 5    Apfel       vorraetig
#> 6 Erdbeere       vorraetig

# Elemente in Spalte ind in Booleans umwandeln 
fruechte_df$ind <- fruechte_df$ind == "vorraetig"
# Auf dieselbe Weise kann auch eine neue Spalte hinzugefügt werden 
# fruechte_df$vorraetig <- fruechte_df$ind == "vorraetig"
# Alternativ mit ifelse-Anweisung (--> nächste Woche!)
# fruechte_df$ind <- ifelse(fruechte_df$ind == "vorraetig", TRUE, FALSE)
fruechte_df

#>     values   ind
#> 1    Birne FALSE
#> 2   Orange FALSE
#> 3   Banane FALSE
#> 4     Kiwi  TRUE
#> 5    Apfel  TRUE
#> 6 Erdbeere  TRUE

Der Dataframe ist immer noch nicht ideal. Zum Beispiel sind die Spaltennamen nicht besonders intuitiv und sollten lieber umbenannt werden, und es fehlt noch die Spalte anzahl mit der Anzahl der vorrätigen Früchte. Im folgenden Abschnitt werden Operationen zum Zugriff und zur Transformation von Dataframes vorgestellt, mit denen solche Umformungen umgesetzt werden können.

2.7.2 Operationen auf Dataframes

Spalten umbenennen:

# Option 1
colnames(fruechte_df) <- c("frucht", "vorraetig")

# Option 2
fruechte_df$values <- fruechte_df$frucht
fruechte_df$ind <- fruechte_df$vorraetig

Spalte hinzufügen:

fruechte_df$anzahl <- c(0, 0, 0, 5, 20, 32)
fruechte_df

#>     frucht vorraetig anzahl
#> 1    Birne     FALSE      0
#> 2   Orange     FALSE      0
#> 3   Banane     FALSE      0
#> 4     Kiwi      TRUE      5
#> 5    Apfel      TRUE     20
#> 6 Erdbeere      TRUE     32

Anordnung der Spalten ändern:

fruechte_df <- fruechte_df[c("frucht", "anzahl", "vorraetig")]
fruechte_df

#>     frucht anzahl vorraetig
#> 1    Birne      0     FALSE
#> 2   Orange      0     FALSE
#> 3   Banane      0     FALSE
#> 4     Kiwi      5      TRUE
#> 5    Apfel     20      TRUE
#> 6 Erdbeere     32      TRUE

Zugriff auf eine Spalte über den Namen der Spalte:

# Option 1
fruechte_df$frucht

#> [1] "Birne"    "Orange"   "Banane"   "Kiwi"     "Apfel"    "Erdbeere"

# Option 2
fruechte_df[["frucht"]]

#> [1] "Birne"    "Orange"   "Banane"   "Kiwi"     "Apfel"    "Erdbeere"

Zugriff auf eine Spalte über den Spaltenindex:

fruechte_df[, 1]

#> [1] "Birne"    "Orange"   "Banane"   "Kiwi"     "Apfel"    "Erdbeere"

Zugriff auf eine Zeile:

fruechte_df[1, ]

#>   frucht anzahl vorraetig
#> 1  Birne      0     FALSE

Zugriff auf einzelne Elemente über den Spaltennamen und den Index der Zeile:

# Zugriff auf Element in Spalte "frucht" und Zeile 3
fruechte_df$frucht[3]

#> [1] "Banane"

# Zugriff auf Elemente in Spalte "frucht" und Zeilen 1 und 4
fruechte_df$frucht[c(1, 4)]

#> [1] "Birne" "Kiwi"

# Zugriff auf Elemente in Spalte "frucht" und Zeilen 1 bis 4
fruechte_df$frucht[c(1:4)]

#> [1] "Birne"  "Orange" "Banane" "Kiwi"

Zugriff auf einzelne Elemente über den Spaltenindex und den Zeilenindex:

# Zugriff auf das Element in Zeile 1 und Spalte 2
fruechte_df[1, 2]

#> [1] 0

Bedingter Zugriff auf Zeilen oder Elemente, die eine bestimmte Bedingung erfüllen:

# Zugriff auf alle Zeilen, in denen in der Spalte anzahl der Wert 20 steht
fruechte_df[fruechte_df$anzahl == 20, ]

#>   frucht anzahl vorraetig
#> 5  Apfel     20      TRUE

# Zugriff auf alle Elemente in der Spalte frucht, für die in der Spalte anzahl der Wert 20 steht
fruechte_df$frucht[fruechte_df$anzahl == 20]

#> [1] "Apfel"

# Zugriff auf alle Elemente in der Spalte frucht, für die in der Spalte anzahl ein Wert kleiner als 20 steht
fruechte_df$frucht[fruechte_df$anzahl < 20]

#> [1] "Birne"  "Orange" "Banane" "Kiwi"

Spalte entfernen:

# hier auskommentiert, da wir die Spalte für unser Beispiel behalten wollen
# fruechte_df$anzahl <- NULL

Zugriffsoperationen der Art fruechte_df$frucht[fruechte_df$anzahl == 20] und fruechte_df$frucht[fruechte_df$anzahl < 20] sehen auf den ersten Blick unübersichtlich aus, aber hier passiert im Grunde genau dasselbe, was wir bereits vom bedingten Zugriff auf Vektoren kennen: Zunächst wird der Ausdruck in den eckigen Klammern ausgewertet. Da jede Spalte in einem Dataframe ein Vektor ist, wird dabei wieder der Mechanismus der Vektorisierung aktiviert und der Ausdruck wird zu einem logischen Vektor aus Wahrheitswerten evaluiert. In diesem Vektor steht TRUE, wenn ein Element in der Spalte fruechte_df$anzahl genau 20 bzw. kleiner als 20 ist, und FALSE sonst. Mit der Zugriffsoperation fruechte_df$frucht[] wird dann auf alle Elemente in der Spalte frucht zugegriffen, für die in der Spalte anzahl in derselben Zeile ein Wert genau 20 bzw. kleiner 20 steht.

Da die Spalten eines Dataframes Vektoren sind, können auf die Spalten alle Operationen angewandt werden, die auch auf Vektoren angewandt werden können, zum Beispiel:

fruechte_df$anzahl * 3

#> [1]  0  0  0 15 60 96

Dataframes können auch kombiniert werden. Wir haben ja bereits beim Erstellen von Matrizen aus bereits existierenden Vektoren die Funktionen rbind() und cbind() verwendet.

neue_fruechte <- data.frame(frucht = c("Apfel", "Zitrone", "Mango"),
                            anzahl = c(20, 15, 0),
                            vorraetig = c(TRUE, TRUE, FALSE)
                 )

# Dataframes zeilenweise kombinieren
rbind(fruechte_df, neue_fruechte)

#>     frucht anzahl vorraetig
#> 1    Birne      0     FALSE
#> 2   Orange      0     FALSE
#> 3   Banane      0     FALSE
#> 4     Kiwi      5      TRUE
#> 5    Apfel     20      TRUE
#> 6 Erdbeere     32      TRUE
#> 7    Apfel     20      TRUE
#> 8  Zitrone     15      TRUE
#> 9    Mango      0     FALSE

# Dataframes spaltenweise kombinieren
cbind(fruechte_df, neue_fruechte)

#>     frucht anzahl vorraetig  frucht anzahl vorraetig
#> 1    Birne      0     FALSE   Apfel     20      TRUE
#> 2   Orange      0     FALSE Zitrone     15      TRUE
#> 3   Banane      0     FALSE   Mango      0     FALSE
#> 4     Kiwi      5      TRUE   Apfel     20      TRUE
#> 5    Apfel     20      TRUE Zitrone     15      TRUE
#> 6 Erdbeere     32      TRUE   Mango      0     FALSE

Achtung: Beachtet, dass beim Zusammenfügen der beiden Dataframes Duplikate entstehen: In dem neuen Dataframe, der mit rbind() erstellt wurde, gibt es zweimal “Apfel”, obwohl sich alle Werte in der Zeile wiederholen. In dem neuen Dataframe, der mit cbind() erstellt wurde, wiederholen sich sogar die Spalten und alle Elemente im Dataframe df_2 werden noch einmal dupliziert. Das hat den Grund, dass cbind() nur Dataframes mit derselben Anzahl an Zeilen zusammenfügen kann.

Um zwei Dataframes so zusammenzufügen, dass gleiche Zeilen nicht dupliziert werden und nur die neuen Zeilen und Spalten hinzugefügt werden, kann die Funktion merge() verwendet werden.

# Dataframes kombinieren und dabei gleiche Spalten zusammenfügen
neue_fruechte <- data.frame(frucht = c("Apfel", "Zitrone", "Mango"),
                            anzahl = c(20, 15, 0),
                            vorraetig = c(TRUE, TRUE, FALSE), 
                            preis = c(2.49, 1.49, .99)
                 )
merge(fruechte_df, neue_fruechte, by=c("frucht","anzahl", "vorraetig"), all = TRUE)

#>     frucht anzahl vorraetig preis
#> 1    Apfel     20      TRUE  2.49
#> 2   Banane      0     FALSE    NA
#> 3    Birne      0     FALSE    NA
#> 4 Erdbeere     32      TRUE    NA
#> 5     Kiwi      5      TRUE    NA
#> 6    Mango      0     FALSE  0.99
#> 7   Orange      0     FALSE    NA
#> 8  Zitrone     15      TRUE  1.49

Im Laufe des Semesters werden wir einige weitere Möglichkeiten kennenlernen, wie Dataframes transformiert und kombiniert werden können.

Verständnisfragen:

Was gilt für alle Spalten eines Dataframes?
Welchen Datentyp haben die Werte in der neuen Spalte vorraetig?
Was passiert, wenn Werte beim Erstellen eines Dataframes fehlen? Löscht einen Wert und probiert es aus.
Verwendet die Funktion View() um euch einen der Dataframes genauer anzusehen. Was passiert?

2.8 Auf einen Blick: Matrizen vs Arrays vs Dataframes

In diesem Abschnitt werden die Unterschiede zwischen Matrizen, Arrays und Dataframes anhand eines Beispiels illustriert. Das Beispiel illustriert, wie Daten zu Temperaturmessungen in drei verschiedenen Städten an drei Tageszeiten mithilfe der verschiedenen Datenstrukturen organisiert werden können.

# Array: Ein dreidimensionales Modell zur Speicherung von Temperaturdaten über eine Woche, gemessen zu verschiedenen Tageszeiten in verschiedenen Städten.
# Ein 3x7x3 Array erstellen für 3 Städte, 7 Tage und 3 Tageszeiten
temperature_array <- array(sample(10:30, 63, replace = TRUE), dim = c(3, 7, 3))
dimnames(temperature_array) <- list(
  Stadt = c("Berlin", "Hamburg", "München"),
  Tag = c("Mo", "Di", "Mi", "Do", "Fr", "Sa", "So"),
  Zeit = c("Morgen", "Mittag", "Abend")
)
print(temperature_array[,"Mo", "Morgen"])

#>  Berlin Hamburg München 
#>      15      22      27

print(temperature_array)

#> , , Zeit = Morgen
#> 
#>          Tag
#> Stadt     Mo Di Mi Do Fr Sa So
#>   Berlin  15 19 30 12 13 28 18
#>   Hamburg 22 14 27 13 21 12 25
#>   München 27 26 17 27 14 15 12
#> 
#> , , Zeit = Mittag
#> 
#>          Tag
#> Stadt     Mo Di Mi Do Fr Sa So
#>   Berlin  14 24 29 26 25 30 24
#>   Hamburg 14 29 19 24 24 11 13
#>   München 11 11 12 24 25 23 24
#> 
#> , , Zeit = Abend
#> 
#>          Tag
#> Stadt     Mo Di Mi Do Fr Sa So
#>   Berlin  14 18 24 12 29 24 18
#>   Hamburg 17 16 24 21 25 17 19
#>   München 23 14 12 26 23 10 24

# Matrix: Die Temperaturmessungen für alle Städte über eine Woche zu einer bestimmten Tageszeit.
morning_temp_matrix <- matrix(temperature_array[ , , "Morgen"], nrow = 7)
rownames(morning_temp_matrix) <- c("Mo", "Di", "Mi", "Do", "Fr", "Sa", "So")
colnames(morning_temp_matrix) <- c("Berlin", "Hamburg", "München")
print(morning_temp_matrix)

#>    Berlin Hamburg München
#> Mo     15      27      14
#> Di     22      17      28
#> Mi     27      12      12
#> Do     19      13      15
#> Fr     14      27      18
#> Sa     26      13      25
#> So     30      21      12

# Dataframe: Die Temperaturmessungen für alle Städte über eine Woche zu einer bestimmten Tageszeit.
morning_temp_dataframe <- data.frame(
  Berlin = temperature_array["Berlin", , "Morgen"],
  Hamburg = temperature_array["Hamburg", , "Morgen"],
  München = temperature_array["München", , "Morgen"]
)
print(morning_temp_dataframe)

#>    Berlin Hamburg München
#> Mo     15      22      27
#> Di     19      14      26
#> Mi     30      27      17
#> Do     12      13      27
#> Fr     13      21      14
#> Sa     28      12      15
#> So     18      25      12

# Der Dataframe sieht auf den ersten Blick genauso aus wie die Matrix. 
# Ein Dataframe kann aber zusätzliche Metadaten und Werte eines anderen Datentyps enthalten:
morning_temp_dataframe$Zeit <- "Morgen"
morning_temp_dataframe$Skala <- "Celsius"
print(morning_temp_dataframe)

#>    Berlin Hamburg München   Zeit   Skala
#> Mo     15      22      27 Morgen Celsius
#> Di     19      14      26 Morgen Celsius
#> Mi     30      27      17 Morgen Celsius
#> Do     12      13      27 Morgen Celsius
#> Fr     13      21      14 Morgen Celsius
#> Sa     28      12      15 Morgen Celsius
#> So     18      25      12 Morgen Celsius

# Wenn wir dasselbe mit der Matrix versuchen, bekommen wir dagegen eine Warnmeldung, und einen wenig sinnvollen Output: 
morning_temp_matrix$Zeit <- "Morgen"

#> Warning in morning_temp_matrix$Zeit <- "Morgen": Coercing LHS to a list

# Auf die Werte in einem Dataframe können auch komplexere Operationen angewandt werden, und die Ergebnisse der Opterationen kann direkt im Dataframe gespeichert werden.
# Wir können zum Beispiel das Maximum für jeden Tag berechenen und eine neue Spalte "Maximum" für diesen Wert übertragen 
morning_temp_dataframe$Maximum <- pmax(morning_temp_dataframe$Berlin, morning_temp_dataframe$Hamburg, morning_temp_dataframe$München)
morning_temp_dataframe

#>    Berlin Hamburg München   Zeit   Skala Maximum
#> Mo     15      22      27 Morgen Celsius      27
#> Di     19      14      26 Morgen Celsius      26
#> Mi     30      27      17 Morgen Celsius      30
#> Do     12      13      27 Morgen Celsius      27
#> Fr     13      21      14 Morgen Celsius      21
#> Sa     28      12      15 Morgen Celsius      28
#> So     18      25      12 Morgen Celsius      25

# Wir könnten auch die Werte in Fahrenheit umwandeln 
morning_temp_dataframe$Maximum <- morning_temp_dataframe$Maximum * 9/5 + 32
morning_temp_dataframe

#>    Berlin Hamburg München   Zeit   Skala Maximum
#> Mo     15      22      27 Morgen Celsius    80.6
#> Di     19      14      26 Morgen Celsius    78.8
#> Mi     30      27      17 Morgen Celsius    86.0
#> Do     12      13      27 Morgen Celsius    80.6
#> Fr     13      21      14 Morgen Celsius    69.8
#> Sa     28      12      15 Morgen Celsius    82.4
#> So     18      25      12 Morgen Celsius    77.0

#... und anschließend die Spalte umbenennen 
morning_temp_dataframe$Maximum_Fahrenheit <- morning_temp_dataframe$Maximum
morning_temp_dataframe$Maximum <- NULL  # entfernt die ursprüngliche "Maximum" Spalte
morning_temp_dataframe

#>    Berlin Hamburg München   Zeit   Skala Maximum_Fahrenheit
#> Mo     15      22      27 Morgen Celsius               80.6
#> Di     19      14      26 Morgen Celsius               78.8
#> Mi     30      27      17 Morgen Celsius               86.0
#> Do     12      13      27 Morgen Celsius               80.6
#> Fr     13      21      14 Morgen Celsius               69.8
#> Sa     28      12      15 Morgen Celsius               82.4
#> So     18      25      12 Morgen Celsius               77.0

# Zur Datenmanipulation werden wir deswegen meist mit Dataframes zu tun haben.

2.9 Datenstrukturen untersuchen

Jetzt haben wir schon ganz schön viele verschiedene Datenstrukturen kennengelernt, da kommt man leicht durcheinander. Letzte Woche haben wir bereits die typeof()-Funktion kennengelernt, um den Datentyp eines Werts herauszufinden. Wenn die Funktion typeof() auf Datenstrukturen angewandt wird, gibt die Funktion Auskunft darüber, wie die Datenstruktur im Speicher abgebildet wird. Ein Dataframe wird im Speicher zum Beispiel immer als Liste repräsentiert:

typeof(morning_temp_dataframe)

#> [1] "list"

Aber wir haben bereits gesehen, dass sich ein Dataframe von einer einfachen Liste unterscheidet. Die Spalten in einem Dataframe müssen immer dieselbe Länge haben und auf Dataframes können andere Funktionen angewandt werden als auf Listen. Um Informationen über die Datenstruktur eines Objekts auf höherer Ebene zu erhalten, kann die Funktion class() verwendet werden:

class(morning_temp_dataframe)

#> [1] "data.frame"

Neben typeof() und class() gibt es noch eine dritte Funktion, mit der die Datenstruktur eines Objekts untersucht werden kann. Die Funktion str() gibt Auskunft über die interne Struktur des Objekts:

str(morning_temp_dataframe)

#> 'data.frame':    7 obs. of  6 variables:
#>  $ Berlin            : int  15 19 30 12 13 28 18
#>  $ Hamburg           : int  22 14 27 13 21 12 25
#>  $ München           : int  27 26 17 27 14 15 12
#>  $ Zeit              : chr  "Morgen" "Morgen" "Morgen" "Morgen" ...
#>  $ Skala             : chr  "Celsius" "Celsius" "Celsius" "Celsius" ...
#>  $ Maximum_Fahrenheit: num  80.6 78.8 86 80.6 69.8 82.4 77

Die Funktion typeof() kann natürlich auch auf einzelne Elemente in einer Datenstruktur angewandt werden:

# Jedes Element hat in einer Matrix hat den Datentyp character
typeof(fruechte_einkauf[1, 1]) # character

#> [1] "character"

# Jede Spalte in einem Dataframe ist ein Vektor
typeof(morning_temp_dataframe[3, ])

#> [1] "list"

# Jede Zeile in einem Dataframe ist eine Liste
typeof(morning_temp_dataframe[, 3])

#> [1] "integer"

Zuletzt gibt es eine Reihe hilfreicher Funktionen, mit denen Datenstrukturen auf bestimmte Aspekte hin untersucht werden können. length() liefert die Anzahl der Elemente in einer Datenstruktur; nchar() gibt die Anzahl der Zeichen in einer Zeichenkette aus. ncol() und nrow() geben Auskunft über die Anzahl an Spalten und Zeilen in einer Datenstruktur und die bereits bekannte Funktion dim() liefert die Dimension. Für Datenstrukturen mit numerischen Werten kann zusätzlich auch das Minimum, das Maximum oder statistische Maße wie der Median oder das arithmetische Mittel bestimmt werden, und zwar mit den Funktionen min(), max(), median(), mean().

Verständnisfragen:

Untersucht die Datenstrukturen aus diesem Kapitel mithilfe der Funktionen typeof(), class(), length(), nchar(), ncol(), nrow() und dim().

Was für ein Wert wird ausgegeben, wenn length() auf einen Dataframe angewendet wird?
Wie hängen ncol(), nrow() und dim() zusammen?
Haben Dataframes auch eine Dimension? Ruft mit ?dim die Dokumentation zur Funktion dim() auf und lest es nach.

2.10 Fehlende und ungültige Werte in Datenstrukturen

Bei der Arbeit mit Daten in R kommt es immer mal vor, dass Werte fehlen oder ungültig sind. In R gibt es spezielle Objekte, die in diesem Fall eingesetzt werden.

Der Wert NULL wird eingesetzt, um die Nicht-Existenz von Daten zu signalisieren. Das haben wir gesehen, als wir mithilfe der Funktion c() einen leeren Vektor erstellt haben. NULL wird außerdem dazu verwendet, um Werte aus Listen oder Dataframes zu entfernen. Wir haben dieses Objekt beispielsweise verwendet, um die Spalte Maximum aus dem Dataframe morning_temp_dataframe zu entfernen.

Daneben gibt es NA, was für Not Available oder “nicht verfügbar” steht und verwendet wird, um das Fehlen von erwarteten Werten in Datenstrukturen zu markieren. Dieser Wert kommt typischerweise in Dataframes zur Anwendung, wenn zu einigen Beobachtungen bestimmte Werte fehlen, zum Beispiel das Alter einer Person in einem Dataframe, der Daten zu verschiedenen Personen enthält.

Zuletzt gibt es den Wert NaN, welcher für Not a Number oder “keine Zahl” steht und signalisiert, dass das Ergebnis einer Berechnung eine undefinierte Zahl ist oder eine Zahl, die nicht repräsentiert werden kann. Ein Beispiel ist das Ergebnis der Operation 0/0.

2.11 Der Mitgliedschaftsoperator %in%

Am Anfang haben wir Datenstrukturen als strukturierte Sammlungen von Werten (oder anderen Objekten) definiert. Um schnell herauszufinden, ob sich ein Wert in einer Datenstruktur befindet, kann ein spezieller Operator verwendet werden: der sogenannte Migliedschaftsoperator %in%. Dieser Operator wird auf Vektoren angewendet: Entweder auf einzelne Vektoren oder auf Vektoren innerhalb einer anderen Datenstruktur, also zum Beispiel auf die Spalten eines Dataframes oder Listenelemente, die Vektoren sind.

Ein paar Beispiele:

buchstaben <- c("a", "b", "c", "f", "s", "g")
"a" %in% buchstaben

#> [1] TRUE

# Es kann auch direkt nach der Mitgliedschaft mehrerer Elemente gefragt werden:
c("a", "f", "b")  %in% buchstaben

#> [1] TRUE TRUE TRUE

# Mitgliedschaftsoperator auf Elemente einer Liste anwenden
obstpreise <- list(obst=c("Apfel", "Banane", "Orange"),
                   preise=c(2.45, 2.99, 1.99))
"Orange" %in% obstpreise$obst

#> [1] TRUE

2.12 Unveränderbarkeit von Objekten in R

Wir haben in der vergangenen Woche besprochen, dass bei der Zuweisung einer Variable ein Wert zugeordnet wird, indem ein Name festgelegt wird, der fortan für diesen Wert und für den Speicherplatz, in dem er gespeichert ist, steht. Der Name ist also sowas wie eine Referenz zu diesem Wert. Aber was passiert eigentlich, wenn der Wert im Programmverlauf verändert wird?

Dieser Frage gehen wir an einem Beispiel nach. Wir weisen zunächst einer Variable x einen Vektor c(1, 2, 3) als Wert zu:

x <- c(1, 2, 3)

Die folgende Grafik aus dem Buch “Advanced R” von Hadley Wickham illustriert, was bei der Zuweisungsoperation passiert:

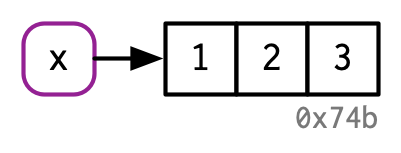
Figure 2.2: Hadley Wickham (2019), https://adv-r.hadley.nz/names-values.html#binding-basics

Der Name x referenziert also nach der Zuweisung einen Vektor mit den Elementen 1, 2 und 3. Die graue Zahl 0x74b steht für die Adresse des Speicherplatzes, der im Computer für das Objekt (den Vektor) “reserviert” ist.

Wenn die Variable x einer neuen Variable y zugewiesen wird, dann referenziert auch der Name y denselben Wert, es entsteht zunächst also keine Kopie des Werts c(1, 2, 3):

y <- x

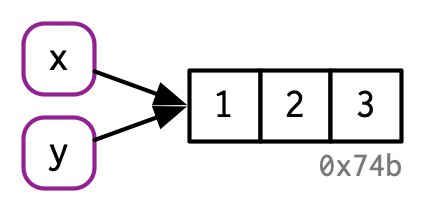
Figure 2.3: Hadley Wickham (2019), https://adv-r.hadley.nz/names-values.html#binding-basics

Aber was passiert mit der Variable x, wenn die Variable y verändert wird? Oder, korrekter formuliert: Welchen Wert referenziert x, wenn mithilfe von y auf den der Wert c(1, 2, 3) zugegriffen und ein Element verändert wird?

x <- c(1, 2, 3)
y <- x
y[3] <- 4 
x

#> [1] 1 2 3

y wird zwar verändert, aber x nicht! Der Wert, der mit y verknüpft ist, wurde verändert, aber das ursprüngliche Objekt nicht. Stattdessen wurde ein neues Objekt erstellt, das eine Kopie des ursprünglichen Objekts mit dem veränderten Wert ist.

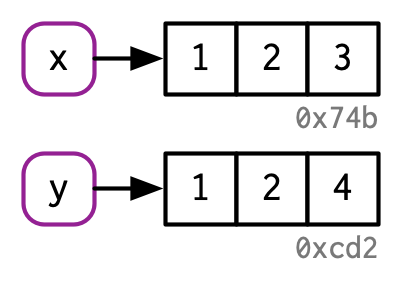
Figure 2.4: Hadley Wickham (2019), https://adv-r.hadley.nz/names-values.html#binding-basics

Dieses Verhalten liegt daran, dass R Objekte unveränderbar, oder auf Englisch immutable sind. Das bedeutet: Wenn wir in R den Wert einer Variable ändern wollen, z.B. x <- x + 1, dann wird tatsächlich ein neues Objekt erstellt und x wird nun auf den neuen Speicherplatz, der den neuen Wert enthält, verwiesen. Der alte Speicherplatz wird freigegeben, wenn keine andere Variable darauf verweist. Bei der Manipulation von Objekten sollte man also dieses Prinzip der Unveränderbarkeit (Immutability) im Hinterkopf behalten, denn hier unterscheidet sich R von anderen Programmiersprachen wie beispielsweise Python.

Diese Beispiele und alle Erklärungen auf Englisch könnt ihr auch nochmal im Kapitel “Binding basics” in Wickhams Lehrbuch “Advanced R” nachlesen. An diesem Punkt sollt ihr aber hauptsächlich das Prinzip der Unveränderbarkeit mal gehört haben; es ist nicht schlimm, wenn ihr den Vorgang nicht im Detail versteht.

Quellen

Venables, W.N. and Smith, D.M. and the R Core Team (2023). An Introduction to R, https://cran.r-project.org/doc/manuals/r-release/R-intro.pdf
Wickham, Hadley. The Tidyverse Style Guide, https://style.tidyverse.org/
Wickham, Hadley (2019). Advanced R. Chapter 4: Subsetting, https://adv-r.hadley.nz/subsetting.html
Wickham, Hadley (2019). Advanced R. Chapter 2: Names and Values, https://adv-r.hadley.nz/names-values.html
Phillips, Nathaniel D. (2018). Matrices and Dataframes, https://bookdown.org/ndphillips/YaRrr/matricesdataframes.html
Phillips, Nathaniel D. (2018). Advanced Dataframe Manipulation, https://bookdown.org/ndphillips/YaRrr/advanceddataframe.html